order of the reaction in an experiment

Chemistry Steps

General Chemistry

Chemical kinetics.

We mentioned in the previous post that the order of a reaction can be determined only by experiment. Most often, this experiment consists of measuring the initial rate of the reaction by changing the concentration of the reactant and monitoring how it affects the rate.

For example, the rate law for a hypothetical reaction where molecule A transforms into products can be written as:

A → Products

Rate = k [A] n

where k is the rate constant and n is the reaction order .

Our objective is to determine the reaction order by calculating the n from a set of experiments. Keep in mind that:

• If n = 0 , the reaction is zero-order, and the rate is independent of the concentration of A.
• If n = 1 , the reaction is first-order , and the rate is directly proportional to the concentration of A.
• If n = 2 , the reaction is second-order , and the rate is proportional to the square of the concentration of A.

Now, suppose we run three experiments, and the following data is obtained for the concentration-rate correlation:

In every experiment, the concentration of A is doubled, and what we see is that the rate of the reaction doubles as well. Therefore, the initial rate is directly proportional to the initial concentration, and thus, we have a first-order reaction :

Rate = k [A] 1

If it was a zero-order reaction , the following data for the concentration-rate relationship would have been obtained:

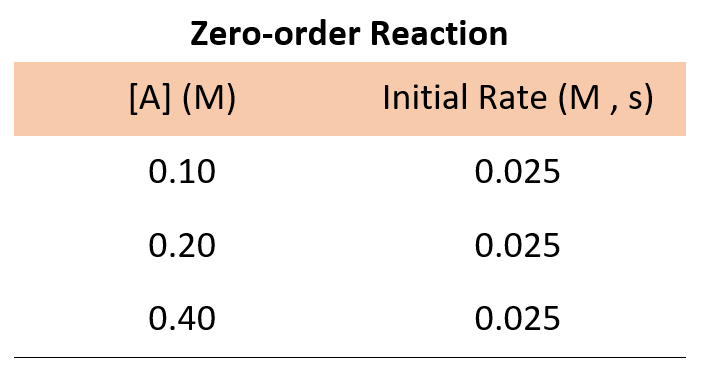
The data for a zero-order reaction indicates that the rate does not depend on the concentration of reactants.

For a second-order reaction , doubling the concertation quadrupoles the reaction rate, and therefore, we would expect the following data:

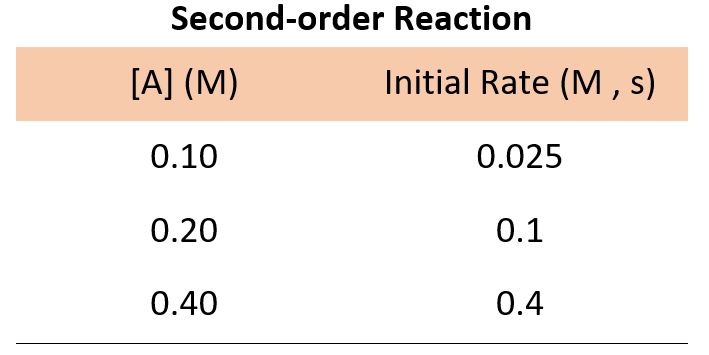
If the numbers are not obvious for determining how the rate changes with concentration, you can pick the data from any set of two experiments, write the rate law, and divide them to see how the rate changes.

For example, going back to the data for a first-order reaction , we can divide the rate of experiments 1 and 2:

\[\frac{{Rate\;2}}{{Rate\;1}}\;{\rm{ = }}\;\frac{{k{{[{{\rm{A}}_2}]}^{\rm{n}}}}}{{k{{[{{\rm{A}}_1}]}^{\rm{n}}}}}\;{\rm{ = }}\;\frac{{{\rm{0}}{\rm{.050}}\;M{\rm{/s}}}}{{{\rm{0}}{\rm{.025}}\,M{\rm{/s}}}}\]

\[\frac{{Rate\;2}}{{Rate\;1}}\;{\rm{ = }}\;\frac{{\cancel{k}{{{\rm{(0}}{\rm{.20}}\,\cancel{M}{\rm{)}}}^{\rm{n}}}}}{{\cancel{k}{{{\rm{(0}}{\rm{.10}}\,\cancel{M}{\rm{)}}}^{\rm{n}}}}}\;{\rm{ = }}\;\frac{{{\rm{0}}{\rm{.050}}\;\cancel{{M{\rm{/s}}}}}}{{{\rm{0}}{\rm{.025}}\,\cancel{{M{\rm{/s}}}}}}\]

\[\frac{{{{{\rm{(0}}{\rm{.20}}\,{\rm{)}}}^{\rm{n}}}}}{{{{{\rm{(0}}{\rm{.10}}\,{\rm{)}}}^{\rm{n}}}}}\;{\rm{ = }}\;2\]

2 n = 2, therefore,

Determining the Value of Rate Constant

To determine the value of the rate constant, write the rate law expression:

Rate = k [A]

Now, you can pick data from any experiment and plug the numbers into a rate law experiment. Let’s use the data from e xperiment 1 .

Rate 1 = k [A 1 ]

\[k\, = \,\frac{{{\rm{rat}}{{\rm{e}}_{\rm{1}}}}}{{\left[ {{{\rm{A}}_{\rm{1}}}} \right]}}\; = \;\frac{{0.025\,M/s}}{{0.10\,M}}\; = \;0.25\,{s^{ – 1}}\]

Let’s now do another example with a real reaction between carbon dioxide and hydrogen and determine the reaction order with respect to each reactant , the overall order , and the value of the rate constant .

Carbon dioxide, CO 2 , reacts with hydrogen to give methanol (CH 3 OH), and water.

CO 2 ( g ) + 3H 2 ( g ) ⇆ CH 3 OH( g ) + H 2 O( g )

In a series of experiments, the following initial rates of disappearance of CO 2 were obtained:

Determine the rate law and calculate the value of the rate constant for this reaction.

To determine the overall reaction order, we need to determine it with respect to both reactants. Let’s first determine the order in CO 2 . Find two experiments where the concentration of H 2 is kept constant while the concentration of CO 2 is changed . In experiments 1 and 2 , the concentration of CO 2 is doubled from 0.640 M to 1.28 M while the concentration of H 2  is kept at 0.220 M . We see from the table, that doubling the concentration of CO 2 quadruples the rate of the reaction (1.08 x 10 -2 ÷ 2.7 x 10 -3 = 4). Therefore, the reaction is   second-order in CO 2 .

Now, let’s find two experiments where the concentration of CO 2 is kept constant while that of H 2  is changed . In experiments 1 and 3 , the concentration of CO 2 is kept at 0640 M while the concentration of H 2  is doubled from 0.220 M to 0.440 M . We see from the table, that doubling the concentration of H 2 had doubled the reaction rate (5.4 x 10 -3 ÷ 2.7 x 10 -3 = 2 ). Therefore, the reaction is  first-order in H 2 .

The rate law, therefore, is:

Rate = k [CO 2 ] 2 [H 2 ]

And the overall order of the reaction is 2+1 = 3 – it is a third-order reaction .

To calculate the value of the rate constant , use the numbers from any experiment for the following equation:

\[k\; = \;\frac{{{\rm{rate}}}}{{{{\left[ {{\rm{C}}{{\rm{O}}_{\rm{2}}}} \right]}^2}\left[ {{{\rm{H}}_{\rm{2}}}} \right]}}\]

\[k\; = \;\frac{{{\rm{2}}{\rm{.7  \times  1}}{{\rm{0}}^{{\rm{ – 3}}}}\;\cancel{{\rm{M}}}{\rm{/s}}}}{{{{\left( {{\rm{0}}{\rm{.640}}\;{\rm{M}}} \right)}^{\rm{2}}}\left( {{\rm{0}}{\rm{.220}}\;\cancel{{\rm{M}}}} \right)}}\;{\rm{ = }}\;{\rm{3}}{\rm{.00 \times 1}}{{\rm{0}}^{{\rm{ – 2}}}}\;{{\rm{M}}^{{\rm{ – 2}}}}{{\rm{s}}^{{\rm{ – 1}}}}\;\]

Here is a 77-question, Multiple-Choice  Quiz on Chemical Kinetics:

Chemical Kinetics Quiz

• Reaction Rate
• Rate Law and Reaction Order
• Integrated Rate Law
• The Half-Life of a Reaction
• Determining the Reaction Order Using Graphs
• Units of Rate Constant k
• How Are Integrated Rate Laws Obtained
• Activation Energy
• The Arrhenius Equation
• Chemical Kinetics Practice Problems

Iron(II) ion is oxidized by hydrogen peroxide in an acidic solution.

2Fe 2 + ( aq ) + H 2 O 2 ( aq ) + 2H + ( aq ) → 2Fe 3+ ( aq ) + 2H2O( l )

The rate law for the reaction is determined to be rate = k [H 2 O 2 ][Fe 2 + ]. The rate constant, at certain temperature, is 2.56 x 10 24 / M · s. Calculate the rate of the reaction at this temperature if [H 2 O 2 ] = 0.48 M and [H 2 O 2 ] = 0.070 M .

For the kinetics of the reaction

 2NO( g ) + Cl 2 ( g ) → 2NOCl( g )

The following data were obtained:

a) What is reaction order in Cl 2 and NO?

b) What is the rate law?

c) What is the value of the rate constant?

The date for the initial rate of the following reaction is listed in the table below:

A + B → C + D

(a) What is the order of reaction with respect to A and to B?

(b) What is the overall reaction order?

(c) What is the value of the rate constant, k ?

Consider the reaction

A(g) + B(g) ⇌ C(g)

The following data were obtained at a certain temperature:

Using the data, determine the order of the reaction and calculate the rate constant:

Leave a Comment Cancel reply

Notify me of followup comments via e-mail. You can also subscribe without commenting.

• Skip to main content
• Skip to secondary menu
• Skip to primary sidebar

Class Notes

Free Class Notes & Study Material

Experimental Determination of Order of a Reaction

Last Updated on July 3, 2023 By Mrs Shilpi Nagpal

• 1.1 (1) Graphical method
• 1.2 (2) Use of integrated rate equation
• 1.3 (3) Initial Rate Method
• 1.4 (4) Ostwald Isolation Method

(1) Graphical method

This method is used when there is only one reactant. It involves the following steps:

1) The concentrations of the reactants are measured by some suitable method.

2) A graph is plotted between concentration and time.

3) The instantaneous rates of the reaction at different times are calculated by finding out the slopes of the tangents corresponding to different times.

4) The rate of reaction is plotted versus concentration,[A] or (concentration) 2 , [A] 2 and so on.

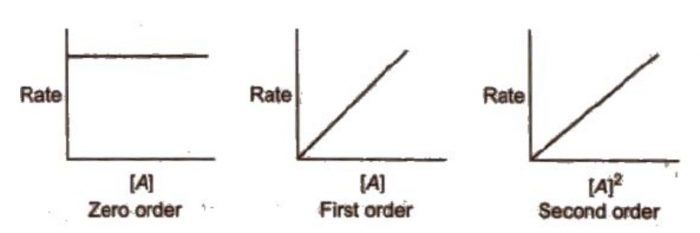
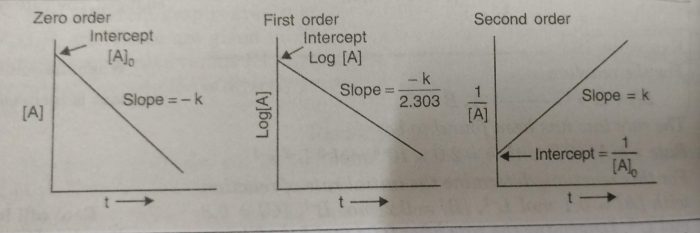
(a) If rate of reaction remains constant in rate versus concentration graph, it means that the rate is independent of the concentration of the reactant, i.e. 

Rate = k [A] 0 = k

Therefore, the reaction is of zero order.

(b) If a straight line is obtained in rate versus concentration graph, it means that the rate is directly proportional to concentration of the reactant i.e.

Rate = k [A] 

Therefore, the reaction is of first order.

(c) If a straight line is obtained in rate versus (concentration) 2 graph, it means that

Rate = k [A] 2

Therefore, the order of the reaction is two.

(d) Similarly, if we get straight line in rate versus (concentration) 3 graph, then

Rate = k[A] 3

and the order of reaction is 3

If we get straight line by plotting graph of rate versus (concentration) n , where n =1, 2, 3…. so on, then 

Rate = k[A] n

and the order of reaction is n.

Example : Decomposition of nitrogen pentoxide.

2N 2 05(g) ——-> 4NO 2 (g) + O 2 (g)

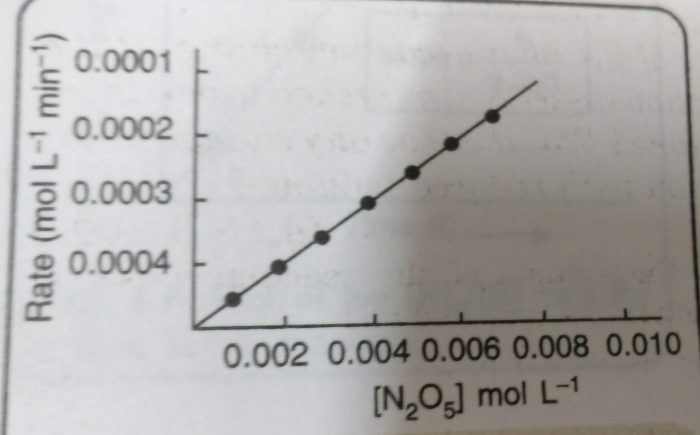
This reaction involves the gaseous reactants and products. Therefore, the reaction can be easily studied by measuring the increase in pressure of the gaseous mixture at different intervals of time. From the measured values of total pressure, the partial pressure of N 2 O 5  at different times can be calculated.

From this, the concentration of N 2 O 5 in moles per litre can be calculated. The molar concentrations of N 2 O 5 obtained are plotted against time. The rates at different times are obtained by measuring the slopes of the tangents corresponding to these times.

Rate = k [N 2 O 5 ] n

The plot of rate versus [N 2 O 5 ] is a straight line.This means that the rate of the reaction is directly proportional to the [N 2 O 5 ]. Therefore, the rate law is:

Rate = k [N 2 O 5 ]

However, we do not get straight line by plotting rate of reaction against [N 2 O 5 ] 2 . This means that the reaction is not of second order.

Rate = -dx/dt = k [N 2 O 5 ]

and order of the reaction is 1.

(2) Use of integrated rate equation

The kinetic data is fitted to different integrated rate equation. Wherever the data fit with the equation for the correct order of the reaction, it will give constant value of rate constant for all data points (concentrations at different times).

For a general reaction:

A ———> Products

the integrated rate equation for zero, first and second order reactions are below given:

The straight lines are obtained for a plot of [A] versus t for a zero order reaction.

(3) Initial Rate Method

The graphical methods cannot be applied for the reaction which involve more than one reactant.The rates of such reactions can be determined by initial rate method.

a) The initial rate of the reaction i.e. the rate at the beginning of the reaction is measured.The rate over an initial time interval that is short enough so that concentration of the reactants do not change appreciably from their initial values.This corresponds to slope of the tangent to the concentration versus time graph at t=0.

b) The initial concentration of only one reactant is changed and the rate is determined again.From this order with respect to that particular reactant is calculated.

c) The procedure is repeated with respect to each reactant until the overall rate law is fully determined.

d) The sum of the individual orders with respect to each reactant gives the order of the reaction.

Consider a reaction

aA + bB + c C ——-> Products

The general form of the rate law may be written as :

Rate = k[A] p [B] q [C] r

Then initial rate of the reaction may be given as :

r 0 = Rate = k [A] 0 p [B] o q [C] o r

If [B] and [C] are kept constant, then

r o = k o [A] o p where k o = k [B] o q [C] o r

The value of p can be determined by inspecting the rate at different values of [A].If we know the initial rates at two different concentration of A.

(r 0 ) 1 =k o [A o ] 1 p

(r 0 ) 2 = k o [A o ] 2 p

where (r 0 ) 1 and (r 0 ) 2 are initial rate of reactions when the initial concentration of A are [A o ] 1 and [A o ] 2

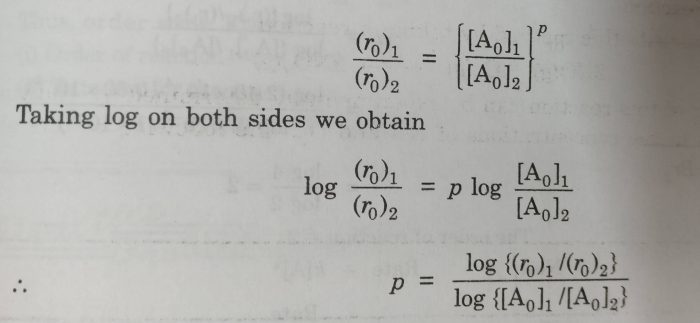
2A + 2B ———> products

Rate = k[A] p [B] q

(Rate) 0 = k [A] o p [B] o q

(4) Ostwald Isolation Method

The total order of the reaction is then equal to the sum of the orders of reaction for individual reactants.This method is based on the principle that if the concentration of all but one reactant are taken in excess , then during the course of the reaction, the concentration of those reactants taken in excess will remain almost constant and hence variation in rate will correspond to the concentration of that reactant whose concentration is small.This process is repeated one by one and order with respect to each reactant is determined.

The overall order will be the sum of all these orders.

aA + bB + c C ———> Products

Suppose we isolate A by taking B and C in large excess and get order of reaction with respect to A.Similarly , we isolate B by taking A and C in B and and C.

Overall order of reaction n= p+ q+ r

About Mrs Shilpi Nagpal

Author of this website, Mrs. Shilpi Nagpal is MSc (Hons, Chemistry) and BSc (Hons, Chemistry) from Delhi University, B.Ed. (I. P. University) and has many years of experience in teaching. She has started this educational website with the mindset of spreading free education to everyone.

Reader Interactions

January 1, 2020 at 4:57 pm

complement of the season, you’ve been a helping hand to me, God bless you and keep it up. HAPPY NEW YEAR

December 14, 2022 at 5:29 pm

Thanks This was really helpful.

Leave a Reply

Your email address will not be published. Required fields are marked *

Now suppose you didn't actually know what the volume V was.

Suppose, for example, that instead of measuring the time taken to collect 5 cm 3 of gas, you just collected the gas up to a mark which you had made on the side of a test tube. Does it matter?

If you are simply wanting to compare initial rates, then it doesn't matter. If you look at the expressions in the table above, you should recognise that the initial rate is inversely proportional to the time taken. In symbols:

In experiments of this sort, you often just use 1/t as a measure of the initial rate without any further calculations.

You can then plot 1/t as a measure of rate against the varying concentrations of the reactant you are investigating. If the reaction is first order with respect to that substance, then you would get a straight line. That's because in a first order reaction, the rate is proportional to the concentration.

If you get a curve, then it isn't first order. It might be second order - but it could equally well have some sort of fractional order like 1.5 or 1.78.

The best way around this is to plot what is known as a "log graph". The maths of this might not be familiar to you, but you may find that you are asked to do this as a part of a practical exam or practical exercise. If it is an exam, you would probably be given help as to how to go about it.

The maths goes like this:

If you have a reaction involving A, with an order of n with respect to A, the rate equation says:

rate = k [A] n

If you take the log of each side of the equation, you get:

log(rate) = log k + n log[A]

If you plotted log(rate) agains log[A], this second equation would plot as a straight line with slope n. If you measure the slope of this line, you get the order of the reaction.

So you would convert all the values you had for rate into log(rate). Convert all the values for [A] into log[A], and then plot the graph. This should be a straight line. If it isn't, then you have done something wrong! Measure the slope to find the order, n.

Note:   Don't worry if you don't understand logs (logarithms), or how I got from the first equation to the second one! I suspect that in the unlikely event of you needing it in an exam at this level, it would be given to you.

All you need to do is find the log button on your calculator and use it to convert your numbers. Practise to start with by trying to find log 2. It should give a value of 0.3010(etc). You probably have to enter 2 and then press the log button, but on some calculators it might be the other way around. If you do it the wrong way around, you will just get an error message.

Some sample reactions

The catalytic decomposition of hydrogen peroxide

This is a simple example of measuring the initial rate of a reaction producing a gas.

A simple set-up to do this might be:

The reason for the weighing bottle containing the catalyst is to prevent introducing errors at the beginning of the experiment. Since this is the part of the reaction you are most interested in, introducing errors here would be stupid!

You have to find a way of adding the catalyst to the hydrogen peroxide solution without changing the volume of gas collected. If you added it to the flask using a spatula, and then quickly put the bung in, you might lose some gas before you got the bung in. Alternatively, as you pushed the bung in, you might force some air into the measuring cylinder. Either way, it makes your results meaningless.

To start the reaction, you just need to shake the flask so that the weighing bottle falls over, and then continue shaking to make sure the catalyst mixes evenly with the solution.

You could also use a special flask with a divided bottom, with the catalyst in one side, and the hydrogen peroxide solution in the other. They are easy to mix by tipping the flask.

If you use a 10 cm 3 measuring cylinder, initially full of water, you can reasonably accurately record the time taken to collect a small fixed volume of gas.

You could, of course, use a small gas syringe instead.

If you were looking at the effect of the concentration of hydrogen peroxide on the rate, then you would have to change its concentration, but keep everything else constant.

The temperature would have to be kept constant, so would the total volume of the solution and the mass of manganese(IV) oxide. You would also have to be sure that the manganese(IV) oxide used always came from the same bottle so that its state of division was always the same.

You could, of course, use much the same apparatus to find out what happened if you varied the temperature, or the mass of the catalyst, or the state of division of the catalyst.

The thiosulphate-acid reaction

If you add dilute hydrochloric acid to sodium thiosulphate solution, you get the slow formation of a pale yellow precipitate of sulphur.

There is a very simple, but very effective, way of measuring the time taken for a small fixed amount of precipitate to form. Stand the flask on a piece of paper with a cross drawn on it, and then look down through the solution until the cross disappears.

So . . . you put a known volume of sodium thiosulphate solution in a flask. Then you add a small known volume of dilute hydrochloric acid, start timing, swirl the flask to mix everything up, and stand it on the paper with the cross on. Time how long it takes for the cross to disappear.

Then repeat using a smaller volume of sodium thiosulphate, but topped up to the same original volume with water. Everything else should be exactly as before.

If you started with, say, 50 cm 3 of sodium thiosulphate solution, you would repeat the experiment with perhaps, 40, 30, 20, 15 and 10 cm 3 - each time made up to a total of 50 cm 3 with water.

The actual concentration of the sodium thiosulphate doesn't have to be known. In each case, you could record its relative concentration. The solution with 40 cm 3 of sodium thiosulphate solution plus 10 cm 3 of water has a concentration which is 80% of the original one, for example. The one with 10 cm 3 of sodium thiosulphate solution plus 40 cm 3 of water has a concentration which is 20% of the original one.

When you came to plotting a rate against concentration graph, as we looked at further up the page, you would plot 1/t as a measure of the rate, and volume of sodium thiosulphate solution as a measure of concentration. Alternatively, you could plot relative concentrations - from, say, 20% to 100%. It doesn't actually matter - the shape of the graph will be identical.

You could also look at the effect of temperature on this reaction, by warming the sodium thiosulphate solution before you added the acid. Take the temperature after adding the acid, though, because the cold acid will cool the solution slightly.

This time you would change the temperature between experiments, but keep everything else constant. To get reasonable times, you would have to use a diluted version of your sodium thiosulphate solution. Using the full strength solution hot will produce enough precipitate to hide the cross almost instantly.

Iodine clock reactions

There are several reactions which go under the name "iodine clock". They are all reactions which give iodine as one of the products. This is the simplest of them, but only because it involves the most familiar reagents.

The reaction we are looking at is the oxidation of iodide ions by hydrogen peroxide under acidic conditions.

The iodine is formed first as a pale yellow solution darkening to orange and then dark red, before dark grey solid iodine is precipitated.

There is a very clever way of picking out a when a particular very small amount of iodine has been formed.

Iodine reacts with starch solution to give a very deep blue solution. If you added some starch solution to the reaction above, as soon as the first trace of iodine was formed, the solution would turn blue. That doesn't actually help!

However, iodine also reacts with sodium thiosulphate solution.

If you add a very small amount of sodium thiosulphate solution to your reaction mixture (including the starch solution), it will react with the iodine that is initially produced, and so the iodine won't affect the starch, and you won't get any blue colour.

However, when that small amount of sodium thiosulphate has been used up, there is nothing to stop the next lot of iodine produced from reacting with the starch. The mixture suddenly goes blue.

Note:   There is a neat piece of video on YouTube showing an iodine clock reaction (not necessarily the one I am talking about here, but it doesn't matter).

It shows three reactions side by side:

The right-hand one is done at room temperature.

The left-hand one is also done at room temperature, but at three times the concentration of one of the reagents.

The central one is colder than room temperature, and presumably at the same concentration as the right-hand one.

The blue colours appear in exactly the order you would predict.

In our example, you could obviously look at the effect of changing the hydrogen peroxide concentration, or the iodide ion concentration, or the hydrogen ion concentration - each time, of course, keeping everything else constant.

That would let you find the orders with respect to everything taking part in the reaction.

Following the course of a single reaction

Rather than doing a whole set of initial rate experiments, you can also get information about orders of reaction by following a particular reaction from start to finish.

There are two different ways you can do this. You can take samples of the mixture at intervals and do titrations to find out how the concentration of one of the reagents is changing. Or (and this is much easier!) you can measure some physical property of the reaction which changes as the reaction continues - for example, the volume of gas produced.

We need to look at these two different approaches separately.

Sampling the reaction mixture

Bromoethane reacts with sodium hydroxide solution as follows:

During the course of the reaction, both bromoethane and sodium hydroxide will get used up. However, it is relatively easy to measure the concentration of the sodium hydroxide at any one time by doing a titration with some standard acid - for example, with hydrochloric acid of a known concentration.

You start with known concentrations of sodium hydroxide and bromoethane, and usually it makes sense to have them both the same. Because the reaction is 1:1, if the concentrations start the same as each other, they will stay the same as each other all through the reaction.

So all you need to do is to take samples using a pipette at regular intervals during the reaction, and titrate them with standard hydrochloric acid in the presence of a suitable indicator.

That is a lot easier said than done!

The problem is that the reaction will still be going on in the time it takes for you to do the titration. And, of course, you only get one attempt at the titration. By the time you take another sample, the concentration of everything will have changed!

There are two ways around this.

You can slow the reaction down by diluting it, adding your sample to a larger volume of cold water before you do the titration. Then do the titration as quickly as possible. That's most effective if you are doing your reaction at a temperature above room temperature. Cooling it as well as diluting it will slow it down even more.

But if possible (and it is possible in the case we are talking about) it is better to stop the reaction completely before you do the titration.

In this case, you can stop it by adding the sample to a known volume (chosen to be an excess) of standard hydrochloric acid. That will use up all the sodium hydroxide in the mixture so that the reaction stops.

Now you would titrate the resulting solution with standard sodium hydroxide solution, so that you can find out how much hydrochloric acid is left over in the mixture.

That lets you calculate how much was used up, and so how much sodium hydroxide must have been present in the original reaction mixture.

This sort of technique is known as a back titration . These calculations can be quite confusing to do without some guidance. If you are interested, you will find back titrations discussed on pages 72-75 of my chemistry calculations book .

Processing the results

You will end up with a set of values for concentration of (in this example) sodium hydroxide against time. The concentrations of the bromoethane are, of course, the same as these if you started with the same concentrations of each reagent.

You can plot these values to give a concentration-time graph which will look something like this:

Now it all gets pretty tedious!

You need to find the rates of reaction at a number of points on the graph, and you do this by drawing tangents to the graph, and measuring their slopes.

You would then draw up a simple table of rate against concentration.

The quickest way to go on from here is to plot a log graph as described further up the page. You would convert all your rates into log(rate), and all the concentrations into log(concentration). Then plot log(rate) against log(concentration).

The slope of the graph gives you the order of reaction.

In our example of the reaction between bromoethane and sodium hydroxide solution, the order would turn out to be 2.

Notice that this is the overall order of the reaction - not just the order with respect to the reagent whose concentration you were measuring. The rate of reaction was falling because the concentrations of both of the reactants were falling.

Note:   This all takes ages to do - not just the practical which would probably take at least an hour, but all the graph drawing, and processing the results from the graphs. There is no obvious way this could be asked in any normal practical or written exam at this level.

I can see that it is just possible that you might be asked in principle how you would do it, but actually doing it could only reasonably be a part of a coursework exercise.

Following the course of the reaction using a physical property

An example where a gas is given off

A familiar example of this is the catalytic decomposition of hydrogen peroxide that we have already looked at above as an example of an initial rate experiment.

This time, you would measure the oxygen given off using a gas syringe, recording the volume of oxygen collected at regular intervals.

So the practical side of this experiment is straightforward, but the calculation isn't.

The problem is that you are measuring the volume of product, whereas to find an order of reaction you have to be working in terms of the concentration of the reactants - in this case, hydrogen peroxide.

That means that you will have to work out the concentration of hydrogen peroxide remaining in the solution for each volume of oxygen you record. To do this, you have to be happy with calculations involving the ideal gas law, and also basic mole calculations.

Having got a table of concentrations against time, you will then process them in exactly the same way as I described above. Plot the graph, draw tangents to find rates at various concentrations, and then plot a log graph to find the order.

Note:   It seems to me fairly unlikely that you could ever be asked to do this in an exam situation. And, at this level, you would almost certainly be given some guidance with the calculations

In a practical exam, few schools could provide a class set of the very expensive gas syringes accurate enough to produce meaningful results, and the time taken to process the results would be far greater than was available in any normal exam. That is equally true of a theory paper.

If you know that you can follow the course of a reaction which produces a gas using this method, that is probably all you will need. But check your syllabus, and past papers and mark schemes.

Colorimetry

In any reaction involving a coloured substance (either reacting or being produced), you can follow the course of the reaction using a colorimeter.

All of this is contained in one fairly small box.

The colour of the light can be changed by selecting a particular coloured filter (or using some more sophisticated device like a diffraction grating). The colour is chosen so that it is the frequency of light which is absorbed by the sample.

Taking copper(II) sulphate solution as a familiar example, you would choose to use a red filter, because copper(II) sulphate solution absorbs red light. The more concentrated the solution is, the more of the red light it will absorb.

Note:   For an explanation of why absorbing red light makes copper(II) sulphate solution blue, see the first part of the page about the colours of complex metal ions . You don't need to read about the origin of the colour for now.

A commonly quoted example of the use of colorimetry in rates of reaction is the reaction between propanone and iodine in the presence of an acid catalyst.

The solution of iodine in propanone starts off brown, and then fades through orange to yellow to colourless as the iodine is used up.

A colorimeter lets you measure the amount of light which is absorbed as it passes through a solution - recorded as the absorbance of the solution.

It is common to plot a calibration curve for a colorimeter by making up solutions of the coloured substance of known concentration and then measuring the absorbance of each under the same conditions as you will do the experiment. You then plot a graph of absorbance against concentration to give your calibration curve.

During your rate of reaction experiment, you read the absorbance from the meter at regular intervals, and then use your calibration curve to convert those values into concentrations.

Then you are faced with the same graphical methods as before.

Note:   In truth, these days, you are more likely to plug your colorimeter into a computer with the right software to do it all for you!

Two other methods

pH measurements

If you have a reaction in which hydrogen ions are reacting or being produced, in principle you should be able to follow changes in their concentration using a pH meter.

You may be aware that pH is a measure of hydrogen ion concentration, and it isn't difficult to calculate an actual hydrogen ion concentration from a pH.

However, if you are measuring pH over a fairly narrow range of hydrogen ion concentrations, the pH doesn't change all that much.

For example, the pH of a solution containing 0.2 mol dm -3 H + has a pH of 0.70. By the time that the concentration has fallen to 0.1 mol dm -3 , the pH has only increased to 1.00.

Whether it is feasible to use a pH meter obviously depends on how accurate it is. If the pH meter only recorded to 0.1 pH units, your results aren't going to be very good.

Conductivity measurements

The electrical conductivity of a liquid depends on the number of ions present, and the nature of the ions. For example, we looked at this reaction much further up the page:

During the course of the reaction, as hydrogen ions and iodide ions get used up, the conductivity of the mixture will fall.

Note:   I am not giving any more detail on this, because conductivity measurements aren't a part of any of the syllabuses that I am tracking. CIE expect you to know that it is possible to use conductivity measurements to follow the course of a reaction involving changes in the ions present, but not how you would actually carry out the experiments or process the results.

Where would you like to go now?

To the rates of reaction menu . . .

To the Physical Chemistry menu . . .

To Main Menu . . .

© Jim Clark 2011 (modified October 2013)

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

3.3.3: Reaction Order

• Last updated
• Save as PDF
• Page ID 1436

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

The reaction order is the relationship between the concentrations of species and the rate of a reaction.

Introduction

The order of a rate law is the sum of the exponents of its concentration terms. Once the rate law of a reaction has been determined, that same law can be used to understand more fully the composition of the reaction mixture. More specifically, the reaction order is the exponent to which the concentration of that species is raised, and it indicates to what extent the concentration of a species affects the rate of a reaction, as well as which species has the greatest effect. For the N 2 O 5 decomposition with a rate law of k[ N 2 O 5 ], this exponent is 1 (and thus is not explicitly shown); this reaction is therefore a first order reaction. It can also be said that the reaction is "first order in N 2 O 5 ". For more complicated rate laws, the overall reaction order and the orders with respect to each component are used. As an example, consider the following reaction,

\[ A + 3B + 2C \rightarrow \text{products} \nonumber \]

whose experimental rate law is given by:

\[\text{rate} = k[A][B]^2 \nonumber \]

This reaction is third-order overall, first-order in A, second-order in B, and zero-order in C.

Zero-order means that the rate is independent of the concentration of a particular reactant. Of course, enough C must be present to allow the equilibrium mixture to form.

Relation to Rate Law

For the reaction:

\[ aA + bB \longrightarrow P \nonumber \]

The rate law is as follows:

\[ rate=k[A]^x[B]^y \nonumber \]

• [A] is the concentration of species A,
• x is the order with respect to species A.
• [B] is the concentration of species B,
• y is the order with respect to species B
• k is the rate constant.
• n is the reaction order for the whole chemical reaction. This can be found by adding the reaction orders with respect to the reactants. In this case, n = x + y.

Simple Rules

The order of a reaction is not necessarily an integer. The following orders are possible:

• Zero: A zero order indicates that the concentration of that species does not affect the rate of a reaction
• Negative integer: A negative order indicates that the concentration of that species INVERSELY affects the rate of a reaction
• Positive integer: A positive order indicates that the concentration of that species DIRECTLY affects the rate of a reaction
• Non-Integer: Non-integer orders, both positive and negative, represent more intricate relationships between concentrations and rate in more complex reactions.

The rate of oxidation of bromide ions by bromate in an acidic aqueous solution,

\[6H^+ + BrO_3^– + 5Br^– \rightarrow 3 Br_2 + 3 H_2O \nonumber \]

is found to follow the following rate law:

\[\text{rate} = k[Br^-][BrO_3^-][H^+]^2 \nonumber \]

What happens to the rate if, in separate experiments, (a) [ BrO 3 – ] is doubled; (b) the pH is increased by one unit; (c) the solution is diluted to twice its volume, with the pH held constant using a buffer?

• Because the rate is first-order in bromate, doubling its concentration doubles the reaction rate.
• Increasing the pH by one unit decreases the [H + ] by a factor of 10. Because the reaction is second-order in [H + ], this decreases the rate by a factor of 100.
• Dilution reduces the concentrations of both Br 2 and BrO 3 – to half their original values. Doing this to each concentration alone would reduce the rate by a factor of 2, so reducing both concentration reduces the rate by a factor of 4, to (½)×(½) = ¼ of its initial value

Methods to Determining Reaction Order

For chemical reactions that require only one elementary step, the values of x and y are equal to the stoichiometric coefficients of each reactant. For chemical reactions that require more than one elementary step, this is not always the case. However, there are many simple ways of determining the order of a reaction. One very popular method is known as the differential method.

The Differential Method

The differential method, also known as the initial rates method, uses an experimental data table to determine the order of a reaction with respect to the reactants used. Below is an example of a table corresponding with the following chemical reaction:

\[ A + B \longrightarrow P \nonumber \]

When looking at the experiments in the table above, it is important to note factors that change between experiments. In order to determine the reaction order with respect to A, one must note in which experiment A is changing; that is, between experiments 1 and 2. Write a rate law equation based on the chemical reaction above.

This is the rate law:

\[\text{rate} = k[A]^x[B]^y \nonumber \]

Next, the rate law equation from experiment 2 must be divided by the rate law equation for experiment 1. Notice that the [B] y term cancels out, leaving "x" as the unknown variable. Simple algebra reveals that x = 0.

The same steps must be taken for determining the reaction order with respect to B. However, in this case experiments 1 and 3 are used. After working through the problem and canceling out [A] x from the equation, y = 1.

Finding the reaction order for the whole process is the easy addition of x and y: n = 0 + 1. Therefore, n = 1

After finding the reaction order, several pieces of information can be obtained, such as half-life .

Other methods

Other methods that can be used to solve for reaction order include the integration method , the half-life method, and the isolation method .

1. Define "reaction order."

Use the following information to solve questions 2 and 3:

Given the rate law equation:

\[\text{rate} = k[A]^1[B]^2 \nonumber \]

2. Determine: a) the reaction order with respect to A, b) the reaction order with respect to B, and c) the total reaction order for the equation.

3. Assuming the reaction occurs in one elementary step, propose a chemical equation using P as the symbol for your product.

Use the data table below to answer questions 4 and 5:

4. Use the differential method to determine the reaction order with respect to A (x) and B (y). What is the total reaction order (n)?

5. What is the rate constant, k?

• The relationship between the concentrations of species and the rate of a reaction
• a) x = 1, b) y = 2, and c) n = 3
• \( A + 2B \longrightarrow P \)
• x = 0.5 and y = 1.7. n = 2.2
• k = 0.10 M min -1
• Chang, Raymond. (2005). Physical Chemistry for the Biosciences . Sausalito,CA: University Science Books.
• Shagoury, Richard. Chemistry 1A Lecture Book. 4th Ed. Custom Publishing. 2006. Print

• Testimonials
• Differential Rate Laws

by Margaret Summers | Sep 27, 2019 | AP chemistry resources , Chemical kinetics

Methods for determining order of reaction

This section looks at how concentration affects reaction rate. You will learn how to determine the order of a reaction . Reactions are often categorized into first , second , third order , etc. and this information is useful for showing the mathematical relationship between concentrations and rates.

Rate laws may be written using two different but related perspectives:

• A differential rate law
• An integrated rate law

In this section, we will focus on differential rate laws, integrated rate laws will be discussed in detail in the next page. Before we begin, download a flowchart here that will help you navigate this lesson:

Download flowchart >>

• Rate of reaction

The rate of reaction studies how fast a reaction takes place – which is concerned with speed. The study relates the change in concentration (reactant or product) over time elapsed.

[concentration] vs time

Order of reaction

The order of reaction studies how a reaction’s rate is affected by the concentration of each reactant in the reaction. The studies relate to the change in concentration (reactants) to the rate of reaction.

rate vs [concentration]

Differential rate law equation

In calculating order of reaction, we are only interested in the concentration of the reactants and NOT the products.

A very simple reaction A + B → C + D , where A and B are the reactants and C and D are the products, we can find the order of reaction by using the rate equation:

rate = k[A]ᵐ[B]ⁿ

Note that (m and n) are not coefficients of the equation, they are the reaction order of each reactant.

It is important to understand that rate law or rate order of a reaction can only be experimentally obtained.

Determining order of reaction

A simple example experimental data is given below:

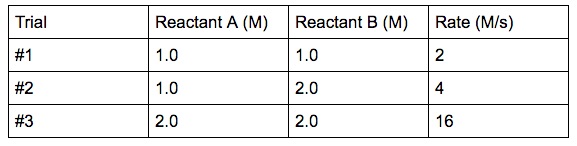
In the experiment, if we vary the concentration of one reactant at a time, we will be able to establish how the rate changes with respect to each reactant.

Reactant A is held constant, the concentration of reactant B is doubled. What is the effect on the rate? (See trial #1 & #2)

Equate the ratio

We can equate the ratio of (change in concentration) to (ratio of change in rate).

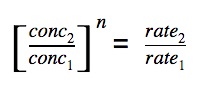
The order of reaction is simply n.

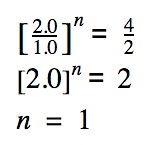
In this case, the order of reaction with respect to reactant B is 1.

The rate order is calculated for one reactant only. Now, we need to calculate the rate order with respect to the other reactant.

The order of reaction with respect to reactant A is calculated as follows:

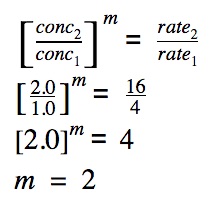
The overall order of reaction

The overall order of reaction is the sum of individual orders of reaction of the reactants.

Overall order of reaction = 3

The rate law for the reaction:

Zeroth order of reaction

The zeroth order reaction does not depend on the concentration of the reactants.

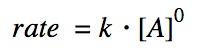
Remember that k is a constant that is dependent on temperature.

Half life is the time it takes for half of the reactant to reach half of its concentration.

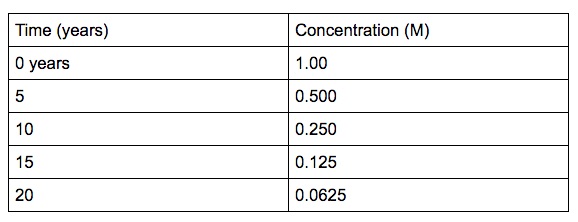
Half life for a 1st order reaction is a constant. A good example of half-life of 1st order reaction is radioactive decay. The concentration of the reactant decreases by a constant with each half – life   and is independent of the concentration of the reactant. The above example shows that the concentration of the reactant decreases by half the amount every 5 years interval.

The half-life of a second-order reaction decreases as the concentration increases.

The half-life of a zeroth-order reaction decreases as the concentration decreases.

Note: Zeroth-order and second-order reactions do not have a constant half-life. Only a 1st order reaction has a constant half-life.

Summary of rate law

Zeroth order : rate does not depend on reactants

First order : rate depends on one 1st order reactant

2nd order : rate depends on two 1st order reactants or one 2nd order reactant

Related posts:

• Mechanisms and Intermediates
• Integrated Rate Laws
• Catalyst and Activation Energy
• 7 Strong Acids: Bringing Chemistry to Life with Humor and Personality7 Strong Acids
• Bonding Spectrum
• How can you determine the number of neutrons in an atom?
• Entropy – Microstate and Macrostate
• Bond Energy and Bond Enthalpy
• Reaction enthalpies
• Reaction Coordinate Diagram
• Memorizing the Names of Polyatomic Ions
• Compounds with Polyatomic Ions
• Flow chart for naming compounds
• Naming inorganic compounds
• Learn the rules for ionic compounds
• Learn the rules for covalent compounds
• Introduction to Chemical Kinetics

Order of Reaction – Definition, Types, Formula and Methods

Order of Reaction: Describes how the concentration of reactants affects the rate. Zero order: rate constant. 1st order: linear. 2nd order: quadratic. Order of reaction has been briefly described here.

Table of Contents

Order of Reaction

The order of a chemical reaction describes how the concentration of reactants affects the reaction rate. In simple terms, it’s like figuring out the recipe for a reaction. Imagine you’re baking cookies and the amount of flour and sugar you use influences how fast the cookies bake. Similarly, in chemistry, the order of reaction reveals how changes in the concentrations of reactant impact the speed of a reaction.

There are different orders: zero-order means the rate is independent of reactant concentration, first-order means the rate is directly proportional to one reactant’s concentration, and second-order indicates a dependence on the square of a reactant’s concentration. Knowing the order helps chemists predict how tweaking ingredients will affect the reaction rate, much like adjusting ingredients in a recipe alters baking time. It’s a way to understand and control chemical processes, making it a crucial concept in the realm of chemical kinetics.

Different Types of Order of Reaction

The order of a chemical reaction defines how the rate of reaction depends on the concentration of reactants. There are three main types of order of reactions namely: zero order reaction, First order reaction, and Second order reaction. These orders can be combined in more complex reactions. The overall order of a reaction is the sum of the individual orders. The order of reaction is determined experimentally by analyzing how the rate changes with varying reactant concentrations.

Zero Order Reaction

A zero-order reaction is a chemical reaction where the rate of reaction is independent of the concentration of the reactants. In simpler terms, the speed at which the reaction occurs doesn’t change, regardless of how much of the reactants are present. It’s like a fixed-speed assembly line; no matter how many workers (reactant molecules) you have, the products are made at a constant rate. Picture a conveyor belt moving at a steady pace – that’s analogous to a zero-order reaction. This reaction type is less common, and the concentration of the reactants remains constant over time, making it distinct from other reaction orders where concentration influences the reaction rate.

First Order Reaction

A first-order reaction describes a chemical process where the rate of reaction depends directly on the concentration of one reactant. In simpler terms, it means that as the concentration of this reactant decreases, the reaction slows down proportionally. The reaction rate is directly proportional to the concentration, implying that if you double the concentration, the rate will also double. Mathematically, the reaction rate (R) is expressed as R = k[A], where ‘k’ is the rate constant and ‘[A]’ is the concentration of the reactant. This type of reaction is common in scenarios like radioactive decay or certain chemical decompositions, providing a fundamental understanding of how reactions progress over time.

Second Order Reaction

A second-order reaction describes a chemical process where the rate of reaction is directly proportional to the square of the concentration of one reactant. In simpler terms, as the concentration of this reactant decreases, the rate of reaction diminishes even more rapidly compared to a first-order reaction. Mathematically, the reaction rate (R) is expressed as R = k[A]^2, where ‘k’ is the rate constant and ‘[A]’ is the concentration of the reactant. This type of reaction often involves two molecules colliding simultaneously for the reactions to occur. Second-order reactions are relevant in various contexts, such as chemical kinetics, where understanding how reactants interact and transform over time is crucial.

Characteristics of Order of Reaction

Understanding the order of reaction is crucial for predicting how changes in reactant concentrations will affect the reaction rate. The characteristics of an order of reaction include:

• Definition: The order of reaction defines how the rate of chemical reaction depends on the concentration of reactants.
• Mathematical Expression: It is expressed as a mathematical power, often denoted as “n”, a representation of the order with respect to a specific reactant. The overall order is the sum of individual orders.
• Units: The order of reaction is dimensionless and doesn’t have any specific units.
• Experimental Determination: Determined experimentally by analyzing how changes in reactant concentration affect the reaction rate.
• Reaction Rate Equation: The rate equation expresses the relationship between the rate of reaction and the concentrations of reactants raised to their respective order.
• Possible Values: The order can be zero, first, second, or even fractional or negative, depending on the reaction kinetics observed.
• Effect on Rate: The order influences how changes in reactant concentrations impact the rate of the reaction.
• Rate Constant: The rate constant (k) is associated with the overall order and represents the rate of reaction under specific conditions.

Different Methods to be Followed in Order to Determine the Reaction Order

There are several different methods that can be followed in order to determine the reaction order. Remember to perform experiments carefully, use appropriate instructions, and analyze the reaction order reliably.

• Initial Rate Method: Measure the initial rates of the reaction at different concentrations of reactants. The reaction order is determined by analyzing how changes in concentration affect the initial rate.
• Integrated Rate Laws: Integrate the rate equation with respect to concentration over time. Different reaction orders yield different integrated rate laws, helping to identify the correct order.
• Half-Life Method: Determine the half-life of the reaction at various concentrations. The relationship between half-life and concentration can reveal the reaction order.
• Graphical Methods: Plotting concentration vs. time or concentration vs. reaction rate can provide insights into the reaction order. For example, a straight line in a certain type of plot indicates a specific order.
• Initial Concentration vs. Initial Rate: Analyze how changes in the initial concentrations of reactants impact the initial rate of the reaction. This can help establish the reaction order.

Do watch the video, for a detailed study

Sharing is caring!

Order of Reaction: FAQs

Q1. define the order of reaction.

Ans: Order of reaction determines how concentration affects reaction rate. Zero order has a constant rate. 1st order shows linear dependence, 2nd order displays quadratic dependence.

Q2. What are the different types of order of reaction?

Ans: There are three main types of order of reactions namely: zero order reaction, First order reaction, and Second order reaction.

Hey there! I'm Sonika an experienced content writer. I craft captivating content for students on various events and subjects like chemistry, physics, and biology. Content perfect for young minds eager to explore the depth of education in India. From molecules to ecosystems, I make complex concepts simple and exciting, specializing in school-level education. Let's journey through the fascinating world of education together!

• CBSE Class 12 Syllabus 2024
• CBSE Class 12 Physics Syllabus
• CBSE Class 12 English Syllabus
• CBSE Class 12 Chemistry Syllabus
• CBSE Class 12 Maths Syllabus
• CBSE Class 10 Sample Paper 2024-25
• CBSE Class 10 English Sample Paper 2024-25
• CBSE Class 10 Maths Sample Paper 2024-25
• CBSE Class 10 Science Sample Paper 2024-25
• CBSE Class 10 SST Sample Paper 2024-25
• CBSE Class 10 Hindi Sample Paper 2024-25
• NEET Syllabus 2025
• NEET Counselling 2024
• NEET Mock Test 2025

Latest Posts

Important exams.

• JEE Mains 2025
• JEE Advanced 2024
• NIMCET 2024
• AP EAMCET 2024
• TS EAMCET 2024
• AP ECET 2024
• TS ECET 2024
• TS PGECET 2024
• BITSAT 2024
• MHT CET 2024
• AP Polycet 2024
• TS Polycet 2024
• JEECUP 2024
• Bihar Polytechnic 2024
• Jharkhand Polytechnic 2024
• Responsible Disclosure Program
• Cancellation & Refunds
• Terms & Conditions
• Privacy Policy

• 7.3 Rate Laws

Orders of Reaction

The reaction orders in a rate law describe the mathematical dependence of the rate on reactant concentrations. Referring to the generic rate law above, the reaction is m order with respect to A and n order with respect to B . For example, if m = 1 and n = 2, the reaction is first order in A and second order in B . The overall reaction order is simply the sum of orders for each reactant. For the example rate law here, the reaction is third order overall (1 + 2 = 3). A few specific examples are shown below to further illustrate this concept.

The rate law:

describes a reaction that is first order in hydrogen peroxide and first order overall. The rate law:

describes a reaction that is second order in C 4 H 6 and second order overall. The rate law:

describes a reaction that is first order in H + , first order in OH − , and second order overall.

Writing Rate Laws from Reaction Orders An experiment shows that the reaction of nitrogen dioxide with carbon monoxide:

is second order in NO 2 and zero order in CO at 100 °C. What is the rate law for the reaction?

The reaction will have the form: $$rate=k[NO_2]^m[CO]^n$$ We are told the reaction is second order in NO 2 ; thus m = 2. The reaction is zero order in CO; thus n = 0. The rate law is: $$rate=k[NO_2]^2[CO]^0=k[NO_2]^2$$ Remember that any number raised to the zero power is equal to 1, thus [CO] 0 = 1, which is why the CO concentration term may be omitted from the rate law: The concentration of CO has no effect on the rate (that term is always 1) so the rate of reaction is solely dependent on the concentration of NO 2 . A later chapter section on reaction mechanisms will explain how a reactant’s concentration can have no effect on a reaction rate despite being involved in the reaction.

Check Your Learning The rate law for the reaction:

has been determined to be rate = k [NO] 2 [H 2 ]. What are the orders with respect to each reactant, and what is the overall order of the reaction?

Since the power on [NO] in the rate law is 2, order in NO = 2. Since the power on H 2 in the rate law is 1 (implied since no value is written), order in H 2 = 1. This means the overall order = (2 + 1) = 3.

Check Your Learning In a transesterification reaction, a triglyceride reacts with an alcohol to form an ester and glycerol. Many students learn about the reaction between methanol (CH 3 OH) and ethyl acetate (CH 3 CH 2 OCOCH 3 ) as a sample reaction before studying the chemical reactions that produce biodiesel:

The rate law for the reaction between methanol and ethyl acetate is, under certain conditions, determined to be:

What is the order of reaction with respect to methanol and ethyl acetate, and what is the overall order of reaction?

From the rate law, the order in CH 3 OH = 1 and the order in CH 3 CH 2 OCOCH 3 = 0. Overall order is (1 + 0) = 1.

Chemistry Dictionary

A complete A-Z dictionary of chemistry terms.

Are you a chemistry student? Visit A-Level Chemistry to download comprehensive revision materials - for UK or international students!

Order of Reaction

The order of the reaction is a relationship between the rate of a chemical reaction and the concentration of the species.

Definition:

The order of reaction is defined as the power dependence of the rate on the concentration of each reactant.

Once the rate law of a reaction is determined the same law can be used to understand the composition of the reaction mixture completely. In other words, the reaction order is the exponent to which the concentration of the specific species is raised, and it shows to what level the concentration of the species affects the rate of reaction. It also indicates up to which extent the species has a considerable effect. For example, the rate of a first-order reaction is determined only by the concentration of one species in the reaction.

Characteristics of the reaction order:

• Reaction order indicates the number of species whose concentration affects directly the rate of reaction.
• The reaction order is always defined with the assistance of the reactant concentrations (but not with product concentrations).
• Reaction order can be obtained by summing up all the exponents of the concentration terms in the rate expression.
• In the balanced reaction, the order of reaction does not depend on the stoichiometric coefficients corresponds to each species.
• The order of reaction vale can be in an integral form or a fraction or even having a zero value

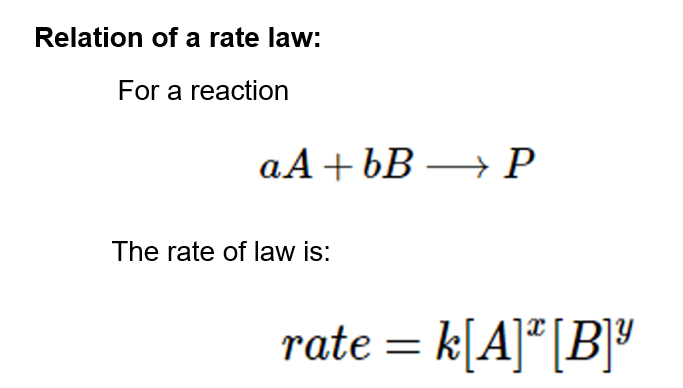
[A] represents the concentration of specie A

[B] represents the concentration of specie B

x indicates the order concerning specie A

y indicates the order concerning specie B

k is known as the rate constant

The exponents x and y are known as partial orders of the reaction. Hence, the sum of all partial orders of the reaction gives the overall order of a reaction.

Units of the rate constant:

The units of a rate constant vary and are dependent on the overall order.

The units of the rate are M/s or Ms -1 .

To determine the units of a rate constant for a specific rate law, divide the units of rate by the units of molarity in the concentration term of the law rate.

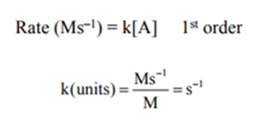
Methods of determining Reaction Order:

There are many ways for determining the order of a reaction. Let’s have a glance at these methods.

• The differential Method:                      

This is one of the easiest methods to obtain the order of a reaction.

• The rate equation of the reaction is written as r= k [A] x [B] y
• by adding the exponents x+y+…… gives us the final value of the reaction order.
• Integral method:

This method is used by taking the order of reaction from the initial rate method.

The concentrations of the reactants that are measured are compared with the integral form of the rate equation.

For example, the integrated rate equation of a first-order reaction is:

ln [A] = -kt + ln [A] 0

where [A] represents the concentration at time t, [A] 0 represents the initial concentration at zero time, k is known as the rate constant and is equal to the slope with a negative sign. The first order law is verified if Ln[A] is a linear function of time.

• Initial rates method:

The natural logarithm of the power-law rate equation is given by:

Ln r =ln k + x ln [A] + y ln [B] + …….

This equation can be used to approximate the order of reaction of each reactant. For example, in a series of experiments the initial rate can be measured at different initial concentrations of the reactant A with every other concentration [B], [C], …… that is kept constant so that the relationship becomes as follows:

                               ln r = x ln [A] + constant

The graph slope of ln r as a function of ln[A] corresponds to the order x concerning reactant A.

This method is however not always reliable because of the following reasons:

the initial rate measurement needs an accurate determination of even a small change in concentration in short times and is sensitive to errors.

Complete determination of the rate equation is not possible if the rate depends on the substances that are not present at the start of the reaction i.e. intermediates/products.

• Flooding method:

In this method, the partial order regarding a given reactant can be calculated. The concentration of a single reactant can be calculated with all other reactants present in large excess; therefore, their concentration will remain constant.

For a reaction a.A + b.B → c.C with the help of rate law: r = k . [A] x. [B] y , the partial order x concerning A is evaluated by using a large excess of B., in this case,

r =k` . [A]x with k’ = k. [B]y ,

Here x can be measured by an integral method while they will be measured with respect to B under the same conditions by a series of same experiments with an initial concentration of a larger range so that the variation in k’ can be calculated.

Different values of Reaction Order:

The value of the order of reaction comes out in different forms like an integer, zero or a fraction. The graph given below explains the reaction rates for different orders.

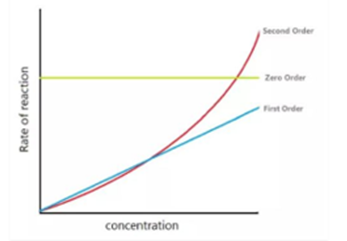
The chemical reactions are divided based upon the dependence of the rate of concentration given below:

• Zero Order Reactions:

A zero-order reaction is considered among one of those whose rate is independent of the concentration.

If there is a change in the concentration of the reactants, it does not affect the speed of the reaction.

Its differential rate law in rate=k. we call these reactions as zeroth-order because it can also be written in such a form that the exponent of the reactant in the rate law is zero.

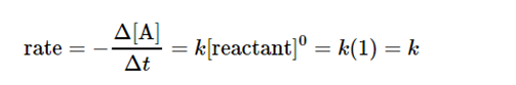
A graph given below between the concentration of reactant and time is a straight line having a slope of –k because the rate is not dependent on reactant concentration. The value of k is negative because with time the concentration of the reactant decreases. On the other hand, a graph between the concentration and time is a straight line having a slope of k, with a positive value.

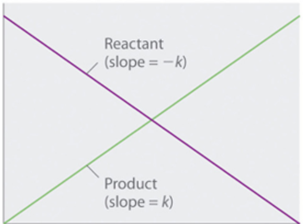
An integrated rate law for a zero-order reaction also gives a straight line and is generally written as:

[A] = [A] 0 – kt

Where [A] 0 is an initial concentration of reactant A. in zero-order reaction, the rate constant has the same units as moles per liter per second.

Many enzymes catalyzed reactions are of zero-order, which says that the reactant concentration is much more than the enzyme concentration which controls the rate so that the enzyme is saturated.

For example, the biological oxidation of ethanol to acetaldehyde by the enzyme is zero order in ethanol.

Similarly, if the catalytic surface is saturated, the heterogeneous catalysis can be zero. For example, on a hot tungsten surface, the decomposition of phosphine (PH 3 ) at high pressure is zero order in phosphine that decomposes at a constant rate.

In homogeneous catalysis, zero-order behaviour can be attained from reversible inhibition. For example, the ring-opening metathesis polymerization used third-generation Grubbs catalyst that exhibits zero-order nature in catalyst because of reversible inhibition that can occur between the pyridine and the ruthenium centre.

• First order:

A first-order reaction is the one in which the rate is directly proportional to the concentration of a single reactant. Consider a liquid reaction

A+B → C + D

The rate equation for this reaction is

As we know the liquid phase reaction is

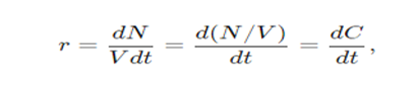
For the above first-order reaction, we have

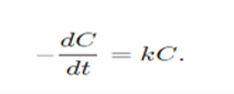
This equation is known as the differential rate equation of the first-order equation. The half-life is independent of the initial concentration and is given by

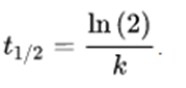
• Second-order reaction:

The reaction is said to be a second-order reaction when the order of a reaction is 2.

The second-order rate reactions can be achieved by squaring the concentration of one reactant or from getting the concentration of two separate reactants.

The rate equation corresponds to

r = k[A]2 or r = [A][B]

NO 2 + CO → NO + CO 2

• Pseudo-First Order Reactions:

In a pseudo-first-order reaction, the concentration of one reactant remains constant and hence it includes the rate constant in the rate expression.

The reactant concentration might be constant as it is present in large amounts when it is compared to the concentration of other reactants or maybe because it is a catalyst.

Consider an elementary reaction

A+ B  → C

Rate expression is given by

– r a = k’ C a C b

If anyone of the reactants i.e. B has a high concentration and there is a small change in the concentration during an entire reaction its value can be supposed to be a constant and we will get a first-order reaction with respect to A. this type of reaction is called a pseudo-first-order reaction:

-r a = (k`C b ) C a = kC a

Where k is a constant.

The second-order reaction requires the determination of the concentration of both the present reactants together. The pseudo-first-order reaction method helps in the study of chemical kinetics.

CH 3 COOCH 3 + H 2 O   → CH 3 COOH + CH 3 OH

This reaction follows pseudo-first-order kinetics because water is present in a considerable amount.

References:

• https://link.springer.com/referenceworkentry/10.1007%2F978-3-642-16712-6_575
• https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_(Physical_and_Theoretical_Chemistry)/Kinetics/Rate_Laws/The_Rate_Law/Reaction_Order
• https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_(Physical_and_Theoretical_Chemistry)/Kinetics/Experimental_Methods/Methods_of_Determining_Reaction_Order
• https://www.chemguide.co.uk/physical/basicrates/orders.html
• https://brilliant.org/wiki/order-of-chemical-reactions/
• https://byjus.com/chemistry/order-of-reaction/

Please rate these notes