what are six steps processes in algorithmic problem solving

Class 8 Syllabus
Maths Notes Class 8
Science Notes Class 8
History Notes Class 8
Geography Notes Class 8
Civics Notes Class 8
NCERT Soln. Class 8 Maths
RD Sharma Soln. Class 8
Math Formulas Class 8

How to Use Algorithms to Solve Problems?

An algorithm is a process or set of rules which must be followed to complete a particular task. This is basically the step-by-step procedure to complete any task. All the tasks are followed a particular algorithm, from making a cup of tea to make high scalable software. This is the way to divide a task into several parts. If we draw an algorithm to complete a task then the task will be easier to complete.

The algorithm is used for,

To develop a framework for instructing computers.
Introduced notation of basic functions to perform basic tasks.
For defining and describing a big problem in small parts, so that it is very easy to execute.

Characteristics of Algorithm

An algorithm should be defined clearly.
An algorithm should produce at least one output.
An algorithm should have zero or more inputs.
An algorithm should be executed and finished in finite number of steps.
An algorithm should be basic and easy to perform.
Each step started with a specific indentation like, “Step-1”,
There must be “Start” as the first step and “End” as the last step of the algorithm.

Let’s take an example to make a cup of tea,

Step 1: Start

Step 2: Take some water in a bowl.

Step 3: Put the water on a gas burner .

Step 4: Turn on the gas burner

Step 5: Wait for some time until the water is boiled.

Step 6: Add some tea leaves to the water according to the requirement.

Step 7: Then again wait for some time until the water is getting colorful as tea.

Step 8: Then add some sugar according to taste.

Step 9: Again wait for some time until the sugar is melted.

Step 10: Turn off the gas burner and serve the tea in cups with biscuits.

Step 11: End

Here is an algorithm for making a cup of tea. This is the same for computer science problems.

There are some basics steps to make an algorithm:

Start – Start the algorithm
Input – Take the input for values in which the algorithm will execute.
Conditions – Perform some conditions on the inputs to get the desired output.
Output – Printing the outputs.
End – End the execution.

Let’s take some examples of algorithms for computer science problems.

Example 1. Swap two numbers with a third variable

Step 1: Start Step 2: Take 2 numbers as input. Step 3: Declare another variable as “temp”. Step 4: Store the first variable to “temp”. Step 5: Store the second variable to the First variable. Step 6: Store the “temp” variable to the 2nd variable. Step 7: Print the First and second variables. Step 8: End

Example 2. Find the area of a rectangle

Step 1: Start Step 2: Take the Height and Width of the rectangle as input. Step 3: Declare a variable as “area” Step 4: Multiply Height and Width Step 5: Store the multiplication to “Area”, (its look like area = Height x Width) Step 6: Print “area”; Step 7: End

Example 3. Find the greatest between 3 numbers.

Step 1: Start Step 2: Take 3 numbers as input, say A, B, and C. Step 3: Check if(A>B and A>C) Step 4: Then A is greater Step 5: Print A Step 6 : Else Step 7: Check if(B>A and B>C) Step 8: Then B is greater Step 9: Print B Step 10: Else C is greater Step 11 : Print C Step 12: End

Advantages of Algorithm

An algorithm uses a definite procedure.
It is easy to understand because it is a step-by-step definition.
The algorithm is easy to debug if there is any error happens.
It is not dependent on any programming language
It is easier for a programmer to convert it into an actual program because the algorithm divides a problem into smaller parts.

Disadvantages of Algorithms

An algorithm is Time-consuming, there is specific time complexity for different algorithms.
Large tasks are difficult to solve in Algorithms because the time complexity may be higher, so programmers have to find a good efficient way to solve that task.
Looping and branching are difficult to define in algorithms.

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

High School
You don't have any recent items yet.
You don't have any courses yet.
You don't have any books yet.
You don't have any Studylists yet.
Information

Stucor CS8451-AA - Notes

Daa (cs8451), anna university.

Recommended for you

Students also viewed.

Hamilton - Good
AD3351 DAA UNIT 4 Notes
CS8451-Design-and-Analysis-of-Algorithms pagenumber
NON recursive algorithm
Cross - Lecture notes 12
CS8451 Design and Analysis of Algorithms QBank (Downloaded from annauniversityedu.blogspot.com)

Preview text

19. What are six steps processes in algorithmic problem solving? [Nov/Dec2009] - Understanding theproblem - Decision making on - Capabilities of computational devices, Choice of exact or approximate problem solving, Datastructures - Algorithmicstrategies - Specification ofalgorithm - Algorithmicverification - Analysis of algorithms

20. What are the basic asymptotic efficiencyclasses? The various basic efficiency classes are - Constant: - Logarithmic: logn - Linear:n - N-log-n: n logn - Quadratic:n - Cubic: n - Exponential:2n - Factorial:n!

21. List the factors which affects the running time of thealgorithm. A. Computer B. Compiler C. Input to thealgorithm i. The content of the input affects the runningtime ii. Typically, the input size is the mainconsideration. 22. Give an non-recursive algorithm to find out the largest element in a list of nnumbers. ALGORITHM MaxElement(A[0.-1])

//Determines the value of the largest element in a given array Input:An array A[0.-1] of real numbers //Output: The value of the largest element in A maxvalïƒŸa[0] for I ïƒŸ 1 to n-1 do if A[I] >maxval return maxvalïƒŸ A[I] return maxval 23. Write a recursive algorithm for computing the nth fibonacci number. ALGORITHM F(n) // Computes the nth Fibonacci number recursively by using the definition // Input A non-negative integer n

// Output The nth Fibonacci number if n 1 return n else return F(n-1)+F(n-2)

24. What is algorithm visualization? Algorithm visualization can be defines as the use of images to convey some useful information about algorithms. Two principal variations are Static algorithm visualization Dynamic Algorithm visualization(also called algorithm animation)

25. What is the order of growth? The Order of growth is the scheme for analyzing an algorithm's efficiency for different input sizes which ignores the multiplicative constant used in calculating the algorithm's running time. Measuring the performance of an algorithm in relation with the input size n is called the order of growth.

PART-B & C

1. Explain about algorithm with suitable example (Notion of algorithm). An algorithm is a sequence of unambiguous instructions for solving a computational problem, i., for obtaining a required output for any legitimate input in a finite amount of time. Algorithms – Computing the Greatest Common Divisor of Two Integers( gcd(m, n): the

largest integer that divides both m and n.)

Euclid9s algorithm: gcd(m, n) = gcd(n, m mod n) Step1: If n = 0, return the value of m as the answer and stop; otherwise, proceed to Step 2. Step2: Divide m by n and assign the value of the remainder to r. Step 3: Assign the value of n to m and the value of r to n. Go to Step 1. Algorithm Euclid(m, n)

//Computes gcd(m, n) by Euclid8s algorithm //Input: Two nonnegative, not-both-zero integers m and n //Output: Greatest common divisor of m and n while n ≠ 0 do r m mod n m n n r return m

About This algorithm

Finiteness: how do we know that Euclid8s algorithm actually comes to a stop Definiteness: nonambiguity Effectiveness: effectively computable.

Consecutive Integer Algorithm

Step1: Assign the value of min{m, n} to t.

Step2: Divide m by t. If the remainder of this division is 0, go to Step3;otherwise, go to Step 4.

In place: A sorting algorithm is in place if it does not require extra memory, except, possibly for a

few memory units.

✓ searching ▪ Find a given value, called a search key, in a given set. ▪ Examples of searching algorithms ➢ Sequential searching ➢ Binary searching... ✓ string processing ▪ A string is a sequence of characters from an alphabet. ▪ Text strings: letters, numbers, and special characters. ▪ String matching: searching for a given word/pattern in a text. ✓ graph problems ▪ Informal definition ➢ A graph is a collection of points called vertices, some of which are connected by line segments called edges. ▪ Modeling real-life problems ▪ Modeling WWW ▪ communication networks ▪ Project scheduling ... Examples of graph algorithms ▪ Graph traversal algorithms ▪ Shortest-path algorithms ▪ Topological sorting ✓ combinatorial problems ✓ geometric problems ✓ Numerical problems

4. Discuss Fundamentals of the analysis of algorithm efficiency elaborately. [Nov/Dec 2019,

Apr/May 2019]

Algorithm8s efficiency

Three notations

Analyze of efficiency of Mathematical Analysis of Recursive Algorithms
Analyze of efficiency of Mathematical Analysis of non-Recursive Algorithms
Analysis of algorithms means to investigate an algorithm9s efficiency with respect to resources: running time and memory space.
Time efficiency: how fast an algorithm runs.
Space efficiency: the space an algorithm requires.
Measuring an input8s size
Measuring running time
Orders of growth (of the algorithm8s efficiency function)
Worst-base, best-case and average efficiency

Measuring Input Sizes

Efficiency is defined as a function of input size.

Input size depends on the problem.

Example 1, what is the input size of the problem of sorting n numbers?

Example 2, what is the input size of adding two n by n matrices?

Units for Measuring Running Time

Measure the running time using standard unit of time measurements, such as seconds, minutes? Depends on the speed of the computer. count the number of times each of an algorithm8s operations is executed. Difficult and unnecessary count the number of times an algorithm8s basic operation is executed. Basic operation: the most important operation of the algorithm, the operation contributing the most to the total running time. For example, the basic operation is usually the most time-consuming operation in the algorithm8s innermost loop.

Orders of Growth consider only the leading term of a formula Ignore the constant coefficient.

Worst-Case, Best-Case, and Average-Case Efficiency Algorithm efficiency depends on the input size n For some algorithms efficiency depends on type of input. Example: Sequential Search

Problem: Given a list of n elements and a search key K, find an element equal to K, if any. Algorithm: Scan the list and compare its successive elements with K until either a matching element is found (successful search) of the list is exhausted (unsuccessful search) Worst case Efficiency Efficiency (# of times the basic operation will be executed) for the worst case input of size n. The algorithm runs the longest among all possible inputs of size n. Best case Efficiency (# of times the basic operation will be executed) for the best case input of size n. The algorithm runs the fastest among all possible inputs of size n. Average case: Efficiency (#of times the basic operation will be executed) for a typical/random input of size n.

NOT the average of worst and best case

5. Elaborate Asymptotic analysis of an algorithm with an example.

Three notations used to compare orders of growth of an algorithm8s basic operation count O( g ( n )): class of functions f ( n ) that grow no faster than g ( n )

A function t(n) is said to be in O(g(n)), denoted t(n)  O(g(n)), if t(n) is bounded above by some

constant multiple of g(n) for all large n , i., if there exist some positive constant c and some

nonnegative integer n 0 such that t(n) <= cg(n) for all n >= n 0

Ω( g ( n )): class of functions f ( n ) that grow at least as fast as g ( n )

A function t(n) is said to be in  (g(n)), denoted t(n)   (g(n)), if t(n) is bounded below by some

Example Recursive evaluation of n ****! (2) ✓ Two Recurrences The one for the factorial function value: F(n) F(n) = F(n 3 1) * n for every n > 0 F(0) = 1 The one for number of multiplications to compute n!, M(n) M(n) = M(n 3 1) + 1 for every n > 0 M(0) = 0 M(n) ∈ Θ (n) 8. Explain in detail about linear search. Sequential Search searches for the key value in the given set of items sequentially and returns the position of the key value else returns -1.

For sequential search, best-case inputs are lists of size n with their first elements equal to a search key; accordingly,

Cbw(n) = 1.

Average Case Analysis:

(a) The standard assumptions are that the probability of a successful search is equal top (0 <= p<- = 1) and (b) the probability of the first match occurring in the ith position of the list is the same for every i. Under these assumptions- the average number of key comparisons Cavg(n) is found as follows. In the case of a successful search, the probability of the first match occurring in the i th position of

the list is p / n for every i, and the number of comparisons made by the algorithm in such a situation

is obviously i. In the case of an unsuccessful search, the number of comparisons is n with the

probability of such a search being (1- p). Therefore

For example, if p = 1 (i., the search must be successful), the average number of key comparisons made by sequential search is (n + 1) /2; i., the algorithm will inspect, on average, about half of the list's elements. If p = 0 (i., the search must be unsuccessful), the average number of key comparisons will be n because the algorithm will inspect all n elements on all such inputs.

8. Write an Algorithm using recursion that determines the GCD of two numbers. Determine the time and space complexity. [Nov/Dec 2019]

Extended Euclidean Algorithm:

Extended Euclidean algorithm also finds integer coefficients x and y such that:

ax + by = gcd(a, b)

Input: a = 30, b = 20

Output: gcd = 10

x = 1, y = -

(Note that 30 1 + 20 (-1) = 10)

Input: a = 35, b = 15

Output: gcd = 5

(Note that 35 1 + 15 (-2) = 5)

The extended Euclidean algorithm updates results of gcd(a, b) using the results calculated by

recursive call gcd(b%a, a). Let values of x and y calculated by the recursive call be x1 and y1. x and

y are updated using the below expressions.

x = y1 - +b/a, * x

Time complexity is log2(max(a,b)) and in good case, if a | b or b|a then time complexity is O (1)

A divide and conquer algorithm works by recursively breaking down a problem into two or more sub-problems of the same (or related) type ( divide ), until these become simple enough to be solved directly ( conquer ). Divide-and-conquer algorithms work according to the following general plan:

A problem is divided into several subproblems of the same type, ideally of about equalsize.
The subproblems are solved (typically recursively, though sometimes a different algorithm is employed, especially when subproblems become smallenough).
If necessary, the solutions to the subproblems are combined to get a solution to theoriginal problem. Example: Merge sort, Quick sort, Binary search, Multiplication of Large Integers and Strassen9s Matrix Multiplication.

8. Write the advantages of insertion sort. [ Nov/Dec 2017] - Simple implementations - Efficient for Small Data Sets - Stable - More efficient - Online

9. Derive the Complexity of Binary Search [Apr/May 2015] In conclusion we are now able completely describe the computing time of binary search by giving formulas that describe the best, average and worst cases.

10. Write about traveling salespersonproblem. Let g = (V, E) be a directed. The tour of G is a directed simple cycle that includes every vertex in V. The cost of a tour is the sum of the cost of the edges on the tour. The traveling salesperson problem to find a tour of minimum cost.

11. What is binarysearch? Binary search is a remarkably efficient algorithm for searching in a sorted array. It works by comparing a search key K with the arrays middle element A[m]. if they match the algorithm stops; otherwise the same operation is repeated recursively for the first half of the array if K < A[m] and the second half if K > A[m]. K >A[0]....[m-1]A[m]A[m+1] A[n-1] search here if KA[m]

12. What is Knapsack problem? [Nov/Dec 2019, Nov/Dec2014] A bag or sack is given capacity and n objects are given. Each object has weight wi and profit pi. Fraction of object is considered as xi (i) 0<=xi<=1 .If fraction is 1 then entire object is put into sack. When we place this fraction into the sack, we get wi xi and pi xi. 13. What is convexhull? Convex Hull is defined as: If S is a set of points then the Convex Hull of S is the smallest convex set containing

Unsuccessful searches

Best case, Average case, Worst case - (log 2 n )

Successful searches

Best case - (1) Average case - (log 2 n ) Worst case - (log 2 n )

14. Write the algorithm for Iterative binarysearch. Algorithm BinSearch(a,n,x) //Given an array a[1:n] of elements in nondecreasing // order, n>0, determine whether x is present { low : = 1; high : = n; while (low < high) do { mid : = [(low+high)/2]; if(x < a[mid]) then high:= mid-1; else if (x >a[mid]) then low:=mid + 1; else return mid; } return 0; }

15. Define internal path length and external pathlength. The internal path length 8I9 is the sum of the distances of all internal nodes from the root. The external path length E, is defines analogously as sum of the distance of all external nodes from the root.

16. Write an algorithm for brute force closest-pair problem. [Nov/Dec2016] Algorithm BruteForceClosestPair(P ) //Finds distance between two closest points in the plane by brute force //Input: A list P of n (n g 2 ) points p 1 (x 1 , y 1 ),... ,pn(xn, yn) //Output: The distance between the closest pair of points d ←∞ for i ←1 to n − 1 do for j ← i + 1 to n do d ←min (d, sqrt((xi − xj ) 2 + (yi − yj ) 2 )) // sqrt is square root return d

17. Design a brute-force algorithm for computing the value of apolynomial P(x) =anxn+an-1 xn-1 + ...+ a 1 x.. 0 at a given point x 0 and determine its worst case efficiency class. Algorithm BetterBruteForcePolynomialEvaluation (P[0.], x) //The algorithm computes the value of polynomial P at a given point x by the <lowest-to- highest //term= algorithm //Input: Array P[0.] of the coefficients of a polynomial of degree n, from the lowest to the //highest, and a number x //Output: The value of the polynomial at the point x p ← P[0]; power ← 1 for i ← 1 to n do

power ← power ∗ x

P ← p + p[i] ∗ power.

Matrix multiplication-Strassen8s algorithm

2. Explain Merge Sort with suitable example. ✓ Merge sort definition**.** Mergesort sorts a given array A[0.-1] by dividing it into two halves a[0..(n/2)-1] and A[n/2.-1] sorting each of them recursively and then merging the two smaller sorted arrays into a single sorted one. ✓ Steps in Merge Sort 1. Divide Step If given array A has zero or one element, return S; it is already sorted. Otherwise, divide A into two arrays, A1 and A2, each containing about half of the elements of A. 2. Recursion Step Recursively sort array A1 and A2. 3. Conquer Step Combine the elements back in A by merging the sorted arrays A1 and A2 into a sorted sequence ✓ Algorithm for merge sort. ALGORITHM Mergesort (A[0.-1]) //Sorts an array A[0.-1] by recursive mergesort //Input: An array A[0.-1] of orderable elements //Output: Array A[0.-1] sorted in nondecreasing order if n > 1 copy A[0..(n/2)-1] to B[0..(n/2)-1] copy A[(n/2).-1] to C[0..(n/2)-1] Mergesort (B[0..(n/2)-1])

Mergesort (C[ ..(n/2)-1]) Merge (B,C,A)

✓ Algorithm to merge two sorted arrays into one. ALGORITHM Merge (B [0.-1], C[0.-1], A[0.+q-1]) //Merges two sorted arrays into one sorted array //Input: arrays B[0.-1] and C[0.-1] both sorted //Output: sorted array A [0.+q-1] of the elements of B & C I 0; j 0; k 0 while I < p and j < q do if B[I] <= C[j] A[k] B [I]; I I+ else A[k] C[j ]; j j+1 k k+ 1 if i = p copy C[j.-1] to A

[k.+q-1] else copy B[i.-1] to A [k.+q-1]

3. Discuss Quick Sort Algorithm and Explain it with example. Derive Worst case and Average Case Complexity. [Apr/May 2019] Quick Sort definition Quick sort is an algorithm of choice in many situations because it is not difficult to implement, it is a good "general purpose" sort and it consumes relatively fewer resources during execution. Quick Sort and divide and conquer

Divide: Partition array A[l.] into 2 subarrays, A[l.-1] and A[s+1.] such that each element of the first array is fA[s] and each element of the second array is g A[s]. (Computing the index of s is part of partition.)
Implication: A[s] will be in its final position in the sorted array.
Conquer: Sort the two subarrays A[l.-1] and A[s+1.] by recursive calls to quicksort
Combine: No work is needed, because A[s] is already in its correct place after the partition is done, and the two subarrays have been sorted. ✓ Steps in Quicksort
Select a pivot w.r. whose value we are going to divide the sublist. (e., p = A[l])
Rearrange the list so that it starts with the pivot followed by a f sublist (a sublist whose elements are all smaller than or equal to the pivot) and a g sublist (a sublist whose elements are all greater than or equal to the pivot ) Exchange the pivot with the last element in the first sublist(i., f sublist) – the pivot is now in its final position
Sort the two sublists recursively using quicksort.

✓ The Quicksort Algorithm ALGORITHM Quicksort(A[l.]) //Sorts a subarray by quicksort //Input: A subarray A[l.] of A[0.-1],defined by its left and right indices l and r //Output: The subarray A[l.] sorted in nondecreasing order if l < r s Partition (A[l.]) // s is a split position Quicksort(A[l.- 1]) Quicksort(A[s+1.] ALGORITHM Partition (A[l .]) //Partitions a subarray by using its first element as a pivot //Input: A subarray A[l.] of A[0.-1], defined by its left and right indices l and r (l < r) //Output: A partition of A[l.], with the split position returned as this function8s value P A[l] i l; j r + 1; Repeat repeat i i + 1 until A[i]>=p //left- right scan repeat j j 3 1 until A[j] <= p//right-left scan

Subset Total weight Total value {1} 2 $ {2} 5 $ {3} 10 $ {4} 5 $ {1,2} 7 $ {1,3} 12 $ {1,4} 7 $ {2,3} 15 $ {2,4} 10 $ {3,4} 15 $ {1,2,3} 17 not feasible {1,2,4} 12 $

6. Write algorithm to find closest pair of points using divide and conquer and explain it with

example. Derive the worst case and average case time complexity. [Nov/Dec 2019]

Following are the detailed steps of a O(n (Logn)^2) algortihm.

Input: An array of n points P[]

Output: The smallest distance between two points in the given array.

As a pre-processing step, the input array is sorted according to x coordinates.

Find the middle point in the sorted array, we can take P[n/2] as middle point.

Divide the given array in two halves. The first subarray contains points from P[0] to P[n/2]. The

second subarray contains points from P[n/2+1] to P[n-1].

Recursively find the smallest distances in both subarrays. Let the distances be dl and dr. Find the minimum of dl and dr. Let the minimum be d.

From the above 3 steps, we have an upper bound d of minimum distance. Now we need to consider

the pairs such that one point in pair is from the left half and the other is from the right half. Consider

the vertical line passing through P[n/2] and find all points whose x coordinate is closer than d to the

middle vertical line. Build an array strip[] of all such points.

Multiple Choice

Course : DAA (CS8451)

University : anna university.

what are six steps processes in algorithmic problem solving

Discover more from: DAA CS8451 Anna University 60 Documents Go to course
More from: DAA CS8451 Anna University 60 Documents Go to course

Chapter: Introduction to the Design and Analysis of Algorithms

Fundamentals of Algorithmic Problem Solving

Let us start by reiterating an important point made in the introduction to this chapter:

We can consider algorithms to be procedural solutions to problems.

These solutions are not answers but specific instructions for getting answers. It is this emphasis on precisely defined constructive procedures that makes computer science distinct from other disciplines. In particular, this distinguishes it from the-oretical mathematics, whose practitioners are typically satisfied with just proving the existence of a solution to a problem and, possibly, investigating the solution’s properties.

We now list and briefly discuss a sequence of steps one typically goes through in designing and analyzing an algorithm (Figure 1.2).

Understanding the Problem

From a practical perspective, the first thing you need to do before designing an algorithm is to understand completely the problem given. Read the problem’s description carefully and ask questions if you have any doubts about the problem, do a few small examples by hand, think about special cases, and ask questions again if needed.

There are a few types of problems that arise in computing applications quite often. We review them in the next section. If the problem in question is one of them, you might be able to use a known algorithm for solving it. Of course, it helps to understand how such an algorithm works and to know its strengths and weaknesses, especially if you have to choose among several available algorithms. But often you will not find a readily available algorithm and will have to design your own. The sequence of steps outlined in this section should help you in this exciting but not always easy task.

An input to an algorithm specifies an instance of the problem the algorithm solves. It is very important to specify exactly the set of instances the algorithm needs to handle. (As an example, recall the variations in the set of instances for the three greatest common divisor algorithms discussed in the previous section.) If you fail to do this, your algorithm may work correctly for a majority of inputs but crash on some “boundary” value. Remember that a correct algorithm is not one that works most of the time, but one that works correctly for all legitimate inputs.

Do not skimp on this first step of the algorithmic problem-solving process; otherwise, you will run the risk of unnecessary rework.

Ascertaining the Capabilities of the Computational Device

Once you completely understand a problem, you need to ascertain the capabilities of the computational device the algorithm is intended for. The vast majority of

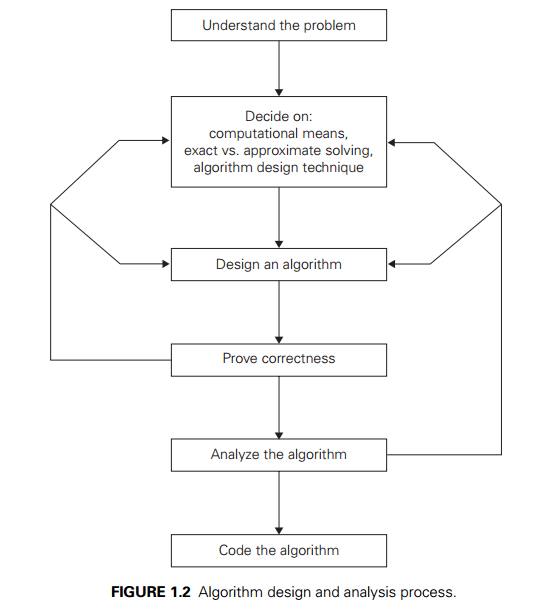
algorithms in use today are still destined to be programmed for a computer closely resembling the von Neumann machine—a computer architecture outlined by the prominent Hungarian-American mathematician John von Neumann (1903– 1957), in collaboration with A. Burks and H. Goldstine, in 1946. The essence of this architecture is captured by the so-called random-access machine ( RAM ). Its central assumption is that instructions are executed one after another, one operation at a time. Accordingly, algorithms designed to be executed on such machines are called sequential algorithms .

The central assumption of the RAM model does not hold for some newer computers that can execute operations concurrently, i.e., in parallel. Algorithms that take advantage of this capability are called parallel algorithms . Still, studying the classic techniques for design and analysis of algorithms under the RAM model remains the cornerstone of algorithmics for the foreseeable future.

Should you worry about the speed and amount of memory of a computer at your disposal? If you are designing an algorithm as a scientific exercise, the answer is a qualified no. As you will see in Section 2.1, most computer scientists prefer to study algorithms in terms independent of specification parameters for a particular computer. If you are designing an algorithm as a practical tool, the answer may depend on a problem you need to solve. Even the “slow” computers of today are almost unimaginably fast. Consequently, in many situations you need not worry about a computer being too slow for the task. There are important problems, however, that are very complex by their nature, or have to process huge volumes of data, or deal with applications where the time is critical. In such situations, it is imperative to be aware of the speed and memory available on a particular computer system.

Choosing between Exact and Approximate Problem Solving

The next principal decision is to choose between solving the problem exactly or solving it approximately. In the former case, an algorithm is called an exact algo-rithm ; in the latter case, an algorithm is called an approximation algorithm . Why would one opt for an approximation algorithm? First, there are important prob-lems that simply cannot be solved exactly for most of their instances; examples include extracting square roots, solving nonlinear equations, and evaluating def-inite integrals. Second, available algorithms for solving a problem exactly can be unacceptably slow because of the problem’s intrinsic complexity. This happens, in particular, for many problems involving a very large number of choices; you will see examples of such difficult problems in Chapters 3, 11, and 12. Third, an ap-proximation algorithm can be a part of a more sophisticated algorithm that solves a problem exactly.

Algorithm Design Techniques

Now, with all the components of the algorithmic problem solving in place, how do you design an algorithm to solve a given problem? This is the main question this book seeks to answer by teaching you several general design techniques.

What is an algorithm design technique?

An algorithm design technique (or “strategy” or “paradigm”) is a general approach to solving problems algorithmically that is applicable to a variety of problems from different areas of computing.

Check this book’s table of contents and you will see that a majority of its chapters are devoted to individual design techniques. They distill a few key ideas that have proven to be useful in designing algorithms. Learning these techniques is of utmost importance for the following reasons.

First, they provide guidance for designing algorithms for new problems, i.e., problems for which there is no known satisfactory algorithm. Therefore—to use the language of a famous proverb—learning such techniques is akin to learning to fish as opposed to being given a fish caught by somebody else. It is not true, of course, that each of these general techniques will be necessarily applicable to every problem you may encounter. But taken together, they do constitute a powerful collection of tools that you will find quite handy in your studies and work.

Second, algorithms are the cornerstone of computer science. Every science is interested in classifying its principal subject, and computer science is no exception. Algorithm design techniques make it possible to classify algorithms according to an underlying design idea; therefore, they can serve as a natural way to both categorize and study algorithms.

Designing an Algorithm and Data Structures

While the algorithm design techniques do provide a powerful set of general ap-proaches to algorithmic problem solving, designing an algorithm for a particular problem may still be a challenging task. Some design techniques can be simply inapplicable to the problem in question. Sometimes, several techniques need to be combined, and there are algorithms that are hard to pinpoint as applications of the known design techniques. Even when a particular design technique is ap-plicable, getting an algorithm often requires a nontrivial ingenuity on the part of the algorithm designer. With practice, both tasks—choosing among the general techniques and applying them—get easier, but they are rarely easy.

Of course, one should pay close attention to choosing data structures appro-priate for the operations performed by the algorithm. For example, the sieve of Eratosthenes introduced in Section 1.1 would run longer if we used a linked list instead of an array in its implementation (why?). Also note that some of the al-gorithm design techniques discussed in Chapters 6 and 7 depend intimately on structuring or restructuring data specifying a problem’s instance. Many years ago, an influential textbook proclaimed the fundamental importance of both algo-rithms and data structures for computer programming by its very title: Algorithms + Data Structures = Programs [Wir76]. In the new world of object-oriented programming, data structures remain crucially important for both design and analysis of algorithms. We review basic data structures in Section 1.4.

Methods of Specifying an Algorithm

Once you have designed an algorithm, you need to specify it in some fashion. In Section 1.1, to give you an example, Euclid’s algorithm is described in words (in a free and also a step-by-step form) and in pseudocode. These are the two options that are most widely used nowadays for specifying algorithms.

Using a natural language has an obvious appeal; however, the inherent ambi-guity of any natural language makes a succinct and clear description of algorithms surprisingly difficult. Nevertheless, being able to do this is an important skill that you should strive to develop in the process of learning algorithms.

Pseudocode is a mixture of a natural language and programming language-like constructs. Pseudocode is usually more precise than natural language, and its usage often yields more succinct algorithm descriptions. Surprisingly, computer scientists have never agreed on a single form of pseudocode, leaving textbook authors with a need to design their own “dialects.” Fortunately, these dialects are so close to each other that anyone familiar with a modern programming language should be able to understand them all.

This book’s dialect was selected to cause minimal difficulty for a reader. For the sake of simplicity, we omit declarations of variables and use indentation to show the scope of such statements as for , if , and while . As you saw in the previous section, we use an arrow “ ← ” for the assignment operation and two slashes “ // ” for comments.

In the earlier days of computing, the dominant vehicle for specifying algo-rithms was a flowchart , a method of expressing an algorithm by a collection of connected geometric shapes containing descriptions of the algorithm’s steps. This representation technique has proved to be inconvenient for all but very simple algorithms; nowadays, it can be found only in old algorithm books.

The state of the art of computing has not yet reached a point where an algorithm’s description—be it in a natural language or pseudocode—can be fed into an electronic computer directly. Instead, it needs to be converted into a computer program written in a particular computer language. We can look at such a program as yet another way of specifying the algorithm, although it is preferable to consider it as the algorithm’s implementation.

Proving an Algorithm’s Correctness

Once an algorithm has been specified, you have to prove its correctness . That is, you have to prove that the algorithm yields a required result for every legitimate input in a finite amount of time. For example, the correctness of Euclid’s algorithm for computing the greatest common divisor stems from the correctness of the equality gcd (m, n) = gcd (n, m mod n) (which, in turn, needs a proof; see Problem 7 in Exercises 1.1), the simple observation that the second integer gets smaller on every iteration of the algorithm, and the fact that the algorithm stops when the second integer becomes 0.

For some algorithms, a proof of correctness is quite easy; for others, it can be quite complex. A common technique for proving correctness is to use mathemati-cal induction because an algorithm’s iterations provide a natural sequence of steps needed for such proofs. It might be worth mentioning that although tracing the algorithm’s performance for a few specific inputs can be a very worthwhile activ-ity, it cannot prove the algorithm’s correctness conclusively. But in order to show that an algorithm is incorrect, you need just one instance of its input for which the algorithm fails.

The notion of correctness for approximation algorithms is less straightforward than it is for exact algorithms. For an approximation algorithm, we usually would like to be able to show that the error produced by the algorithm does not exceed a predefined limit. You can find examples of such investigations in Chapter 12.

Analyzing an Algorithm

We usually want our algorithms to possess several qualities. After correctness, by far the most important is efficiency . In fact, there are two kinds of algorithm efficiency: time efficiency , indicating how fast the algorithm runs, and space ef-ficiency , indicating how much extra memory it uses. A general framework and specific techniques for analyzing an algorithm’s efficiency appear in Chapter 2.

Another desirable characteristic of an algorithm is simplicity . Unlike effi-ciency, which can be precisely defined and investigated with mathematical rigor, simplicity, like beauty, is to a considerable degree in the eye of the beholder. For example, most people would agree that Euclid’s algorithm is simpler than the middle-school procedure for computing gcd (m, n) , but it is not clear whether Eu-clid’s algorithm is simpler than the consecutive integer checking algorithm. Still, simplicity is an important algorithm characteristic to strive for. Why? Because sim-pler algorithms are easier to understand and easier to program; consequently, the resulting programs usually contain fewer bugs. There is also the undeniable aes-thetic appeal of simplicity. Sometimes simpler algorithms are also more efficient than more complicated alternatives. Unfortunately, it is not always true, in which case a judicious compromise needs to be made.

Yet another desirable characteristic of an algorithm is generality . There are, in fact, two issues here: generality of the problem the algorithm solves and the set of inputs it accepts. On the first issue, note that it is sometimes easier to design an algorithm for a problem posed in more general terms. Consider, for example, the problem of determining whether two integers are relatively prime, i.e., whether their only common divisor is equal to 1. It is easier to design an algorithm for a more general problem of computing the greatest common divisor of two integers and, to solve the former problem, check whether the gcd is 1 or not. There are situations, however, where designing a more general algorithm is unnecessary or difficult or even impossible. For example, it is unnecessary to sort a list of n numbers to find its median, which is its n/ 2 th smallest element. To give another example, the standard formula for roots of a quadratic equation cannot be generalized to handle polynomials of arbitrary degrees.

As to the set of inputs, your main concern should be designing an algorithm that can handle a set of inputs that is natural for the problem at hand. For example, excluding integers equal to 1 as possible inputs for a greatest common divisor algorithm would be quite unnatural. On the other hand, although the standard formula for the roots of a quadratic equation holds for complex coefficients, we would normally not implement it on this level of generality unless this capability is explicitly required.

If you are not satisfied with the algorithm’s efficiency, simplicity, or generality, you must return to the drawing board and redesign the algorithm. In fact, even if your evaluation is positive, it is still worth searching for other algorithmic solutions. Recall the three different algorithms in the previous section for computing the greatest common divisor: generally, you should not expect to get the best algorithm on the first try. At the very least, you should try to fine-tune the algorithm you already have. For example, we made several improvements in our implementation of the sieve of Eratosthenes compared with its initial outline in Section 1.1. (Can you identify them?) You will do well if you keep in mind the following observation of Antoine de Saint-Exupery,´ the French writer, pilot, and aircraft designer: “A designer knows he has arrived at perfection not when there is no longer anything to add, but when there is no longer anything to take away.” 1

Coding an Algorithm

Most algorithms are destined to be ultimately implemented as computer pro-grams. Programming an algorithm presents both a peril and an opportunity. The peril lies in the possibility of making the transition from an algorithm to a pro-gram either incorrectly or very inefficiently. Some influential computer scientists strongly believe that unless the correctness of a computer program is proven with full mathematical rigor, the program cannot be considered correct. They have developed special techniques for doing such proofs (see [Gri81]), but the power of these techniques of formal verification is limited so far to very small programs.

As a practical matter, the validity of programs is still established by testing. Testing of computer programs is an art rather than a science, but that does not mean that there is nothing in it to learn. Look up books devoted to testing and debugging; even more important, test and debug your program thoroughly whenever you implement an algorithm.

Also note that throughout the book, we assume that inputs to algorithms belong to the specified sets and hence require no verification. When implementing algorithms as programs to be used in actual applications, you should provide such verifications.

Of course, implementing an algorithm correctly is necessary but not sufficient: you would not like to diminish your algorithm’s power by an inefficient implemen-tation. Modern compilers do provide a certain safety net in this regard, especially when they are used in their code optimization mode. Still, you need to be aware of such standard tricks as computing a loop’s invariant (an expression that does not change its value) outside the loop, collecting common subexpressions, replac-ing expensive operations by cheap ones, and so on. (See [Ker99] and [Ben00] for a good discussion of code tuning and other issues related to algorithm program-ming.) Typically, such improvements can speed up a program only by a constant factor, whereas a better algorithm can make a difference in running time by orders of magnitude. But once an algorithm is selected, a 10–50% speedup may be worth an effort.

A working program provides an additional opportunity in allowing an em-pirical analysis of the underlying algorithm. Such an analysis is based on timing the program on several inputs and then analyzing the results obtained. We dis-cuss the advantages and disadvantages of this approach to analyzing algorithms in Section 2.6.

In conclusion, let us emphasize again the main lesson of the process depicted in Figure 1.2:

As a rule, a good algorithm is a result of repeated effort and rework.

Even if you have been fortunate enough to get an algorithmic idea that seems perfect, you should still try to see whether it can be improved.

Actually, this is good news since it makes the ultimate result so much more enjoyable. (Yes, I did think of naming this book The Joy of Algorithms .) On the other hand, how does one know when to stop? In the real world, more often than not a project’s schedule or the impatience of your boss will stop you. And so it should be: perfection is expensive and in fact not always called for. Designing an algorithm is an engineering-like activity that calls for compromises among competing goals under the constraints of available resources, with the designer’s time being one of the resources.

In the academic world, the question leads to an interesting but usually difficult investigation of an algorithm’s optimality . Actually, this question is not about the efficiency of an algorithm but about the complexity of the problem it solves: What is the minimum amount of effort any algorithm will need to exert to solve the problem? For some problems, the answer to this question is known. For example, any algorithm that sorts an array by comparing values of its elements needs about n log 2 n comparisons for some arrays of size n (see Section 11.2). But for many seemingly easy problems such as integer multiplication, computer scientists do not yet have a final answer.

Another important issue of algorithmic problem solving is the question of whether or not every problem can be solved by an algorithm. We are not talking here about problems that do not have a solution, such as finding real roots of a quadratic equation with a negative discriminant. For such cases, an output indicating that the problem does not have a solution is all we can and should expect from an algorithm. Nor are we talking about ambiguously stated problems. Even some unambiguous problems that must have a simple yes or no answer are “undecidable,” i.e., unsolvable by any algorithm. An important example of such a problem appears in Section 11.3. Fortunately, a vast majority of problems in practical computing can be solved by an algorithm.

Before leaving this section, let us be sure that you do not have the misconception—possibly caused by the somewhat mechanical nature of the diagram of Figure 1.2—that designing an algorithm is a dull activity. There is nothing further from the truth: inventing (or discovering?) algorithms is a very creative and rewarding process. This book is designed to convince you that this is the case.

Exercises 1.2

Old World puzzle A peasant finds himself on a riverbank with a wolf, a goat, and a head of cabbage. He needs to transport all three to the other side of the river in his boat. However, the boat has room for only the peasant himself and one other item (either the wolf, the goat, or the cabbage). In his absence, the wolf would eat the goat, and the goat would eat the cabbage. Solve this problem for the peasant or prove it has no solution. (Note: The peasant is a vegetarian but does not like cabbage and hence can eat neither the goat nor the cabbage to help him solve the problem. And it goes without saying that the wolf is a protected species.)

New World puzzle There are four people who want to cross a rickety bridge; they all begin on the same side. You have 17 minutes to get them all across to the other side. It is night, and they have one flashlight. A maximum of two people can cross the bridge at one time. Any party that crosses, either one or two people, must have the flashlight with them. The flashlight must be walked back and forth; it cannot be thrown, for example. Person 1 takes 1 minute to cross the bridge, person 2 takes 2 minutes, person 3 takes 5 minutes, and person 4 takes 10 minutes. A pair must walk together at the rate of the slower person’s pace. (Note: According to a rumor on the Internet, interviewers at a well-known software company located near Seattle have given this problem to interviewees.)

Which of the following formulas can be considered an algorithm for comput-ing the area of a triangle whose side lengths are given positive numbers a , b , and c ?

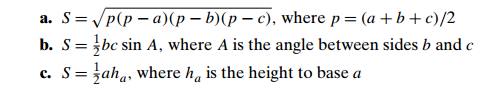
Write pseudocode for an algorithm for finding real roots of equation ax 2 + bx + c = 0 for arbitrary real coefficients a, b, and c. (You may assume the availability of the square root function sqrt (x). )

Describe the standard algorithm for finding the binary representation of a positive decimal integer

in English.

in pseudocode.

Describe the algorithm used by your favorite ATM machine in dispensing cash. (You may give your description in either English or pseudocode, which-ever you find more convenient.)

a. Can the problem of computing the number π be solved exactly?

How many instances does this problem have?

Look up an algorithm for this problem on the Internet.

Give an example of a problem other than computing the greatest common divisor for which you know more than one algorithm. Which of them is simpler? Which is more efficient?

Consider the following algorithm for finding the distance between the two closest elements in an array of numbers.

ALGORITHM MinDistance (A [0 ..n − 1] )

//Input: Array A [0 ..n − 1] of numbers

//Output: Minimum distance between two of its elements dmin ← ∞

for i ← 0 to n − 1 do

for j ← 0 to n − 1 do

if i = j and |A[i] − A[j ]| < dmin dmin ← |A[i] − A[j ]|

return dmin

Make as many improvements as you can in this algorithmic solution to the problem. If you need to, you may change the algorithm altogether; if not, improve the implementation given.

One of the most influential books on problem solving, titled How To Solve It [Pol57], was written by the Hungarian-American mathematician George Polya´ (1887–1985). Polya´ summarized his ideas in a four-point summary. Find this summary on the Internet or, better yet, in his book, and compare it with the plan outlined in Section 1.2. What do they have in common? How are they different?

16 Fundamental Stages of Problem Solving

Fundamental Stages of Problem Solving

This module focuses on the stages of problem solving. The learning objectives of this module are as follows:

To understand stages of Problem solving process
Characteristics of an Efficient Algorithm
To categorize algorithms

Fundamental stages of Problem Solving

Problem solving is both an art and science. As there are no guidelines available to solve the problem, the problem solving is called an art as high creativity is needed for solving problems effectively. Thus by art, we mean one has to be creative, novel and adventurous and by science, we mean the problem solving should be based on sound mathematical and logical guidelines.

The problem solving stages are given as follows:

1. Problem Understanding

2. Algorithm Planning

3. Design of algorithms

4. Algorithm Verification and Validation

5. Algorithm analysis

6. Algorithm Implementation

7. Perform post-mortem analysis

1. Problem Understanding:

Is it possible to solve the given problem? This falls under the domain called computability theory. Computability theory deals with the solvability of the given problem.

To deal with the solvability, one require analytical thinking. Analytical thinking deals with the ways of solving the given problems. It is not possible to solve the problem if the problem is ill- defined. Often puzzles depict the limitations of computing power. Sometimes, there may be some solution but one doesn‟t have the knowledge or means to analyze the algorithms. Thus problems can be as follows:

1. Computationally hard problems: It is not possible to solve this problem.

2. Analytically hard problems: These problems, like Traveling salesperson problem, runs effectively for small instances. But for larger problems, it may be computationally feasible. Also for some problems analysis is difficult.

In computability theory, these sort of problems are often considered. The problem solving starts with understanding of the problem and aims at providing a detailed problem statement. There should not be any confusion in the problem statement. As the mistakes in understanding the problem may affect the development of algorithms.

2. Planning of an algorithm

Once problem statement is produced, the planning of algorithm starts. This phase requires selection of computing model and data structures.

Computational model is the selection of a computing device. A computational model is a mathematical model. Why? It is meaningless to talk about fastness of the algorithm with respect to a particular machine or environment. An algorithm may run faster in machine A compared to machine B. Hence, analysis of algorithms based on a particular brand of machines is meaningless. Hence, the algorithm analysis should be should be independent of machines.

Normally, two theoretical machines are used – One is called Random Access Machine (RAM) and another is called Turing machine.

Data Structures

Second major decision in algorithm planning is selection of a data structure. Data structure is a domain that deals with data storage along with its relationships. Data structures can have impact on the efficiency of the algorithms. Therefore, algorithms and data structures together often constitute important aspect of problem solving.

Fig. 1 : Example of a Queue

Data organization is something we are familiar with in our daily life. The Fig 1 shows a data organization called „Queue”. A Gas station with one servicing point should have a queue like above to avoid chaos. A queue (or FCFS – First Come First Serve) is an organization where the processing (filling of gas) is done in one end and addition of a vehicle is done in another end. A popular statement in computer science is “Algorithm + Data structure = Program” as a wrong selection of a data structure often proves fatal in problem solving.

The planning of a data structure can be based on the solution also as some of the problems can be solved exactly. Sometimes, getting the exact solution is impossible for computationally hard problems. Therefore, for such problems approximate solutions are planned.

2. Design of Algorithms

Algorithm design is the next stage of problem solving. Algorithm design is a way of developing the algorithmic solutions using the appropriate design strategy.

Different types of problem demands different strategies for finding the solution. Just imagine, searching a name in a telephone directory. If one has to search for a name “Qadir”, then the search can be done from starting page to the end page. This is a crude way of solving the problem. Instead, one can prefer to search using indexed entries. It can be done using interpolation search also. Thus design strategy selection plays an important role in solving problems effectively.

After the algorithm is designed, it should be communicated to a programmer so that the algorithms can be coded as a program. This stage is called algorithm specification. The choices of communication can be natural language, programming language and pseudocode. Natural language is preferable, but has some disadvantages such as lack of precision and ambiguity. Programming language may create a dependency on that particular language. Hence, often algorithm is written and communicated through pseudocode. Pseudocode is a mix of natural language and mathematics.

3. Algorithm Verification and validation

Algorithm verification and validation is the process of checking algorithm correctness. An algorithm is expected to give correct output for all valid inputs. This process is called algorithm validation . Once validation is over, program proving or program verification starts .

Verification is done by giving mathematical proofs. Mathematical proofs are rigorous and better than scientific methods. Program correctness itself a major study by itself. Proofs are given as follows:

1. Proof by assertion: Assertion assert some facts. It can be given throughout the program and assertions expressed are in predicate calculus. If it can be proved that, if for every legal input, if it leads to a logical output, then it can be said that the given algorithm is correct.

2. Mathematical Induction: Mathematical induction is a technique can be used to prove recursive algorithms.

5. Algorithm Analysis

Once the algorithm is proved correct, then the analysis starts. Analysis is important for two reasons. They are as follows:

1. To decide efficiency of algorithms

2. To compare algorithms for deciding the effective solutions for a given problem.

Algorithm analysis as a domain is called Algorithmic Complexity theory. What is a complexity? Well, complexity is assumed to be with respect to size of the input. Sorting of an array with 10 numbers is easy: but the same problem with 1 million is difficult. So there is a connection with the complexity and the size of the input.

The complexity of two or more algorithms can be done based on measures that can be categorized into two types.

1. Subjective measures.

2. Objective measures.

Subjective measures include factors like ease of implementation or style of the algorithm or understandability of algorithms. But the problem with the subjective measures are that they vary from person to person. Hence Objective measures are preferable.

Objective measures include factors like time complexity, space complexity and measures like disk usage and network usage. By and large, algorithmic analysis is the estimation of computing resources. Out of all objective measures, two measures are popular. They are time and space.

1. Time complexity: Time complexity refers to the time taken by the algorithm to run for scaled input. By time, it is often meant run time. Actually, there are two time factors. One is execution time and another is run time. Execution (or compile time) does not depend on problem instances and compilers often ignore instances. Hence, time always refers to run or execution time only.

2. Space Complexity : Space complexity is meant the memory required to store the program.

6. Implementation of algorithm as a program and performance analysis

After the algorithms are designed, it is implemented as a program. This stage requires the selection of a programming language. After the program is written, then the program must be tested. Sometimes, the program may not give expected results due to errors. The process of removing the errors is called debugging . Once program is available, they can be verified with a bench mark dataset. It is called experimental algorithmics. This is called performance analysis. Thus, P rofiling is a process of running a program on a datasets and measuring the time/space requirement of the program.

7. Postmortem analysis

A theoretical best solution for the given problem is called lower bound of the algorithm. The worst case estimate of behavior of the algorithm is called upper bound. The difference between upper and lower bound is called algorithmic gap . Technically, no algorithmic gaps should exist. But practically, there may be vast gap present between two bounds. Problem solving process ends with postmortem analysis. Any analysis should end with the valuable insight. Insights like Is the problem solvable? Are there any limits of this algorithm? and Is the algorithm efficient? are asked and collected.

Refining the algorithms is to bring these gaps short by reefing planning, design, implementation and analysis. Thus problem solving is not linear but rather this is a cycle.

Classification of Algorithms

For effective, often algorithms are categorized. The algorithm categorization can be done based on various criteria such as

1. Implementation

3. Problem Types

4. Tractability

1. Classification by Implementation

Based on implementation, one can classify the algorithms as recursive algorithm and iterative algorithms.

Recursive algorithm is an algorithm that uses functions that call itself conditionally. Recursion is a top-down approach of solving the given problem by reducing the problem to another problem with a unit decrease in input instance. The transformed problem is same as the original problem but with a difference that its input is one less than the original problem. This strategy uses the principles of work postponement or delaying the work . Iterative algorithms on the other hand are deductive.

Based on implementation, the algorithms can be classified as sequential or parallel algorithms. An algorithm that uses only one processor is called sequential algorithm. On the other hand, a parallel algorithm uses a set of processors to find a solution of the problem. Similarly, the algorithm can be classified as exact or approximation based on the solution it provides for the given problem. Again, based on implementation, the algorithms can be categorized as deterministic and randomized. Deterministic algorithms have predictable results for a given input. If this is not possible, then the algorithm is called non-deterministic.

2. Classification by Design

Based on design technique, the algorithms can be classified. Some of the popular algorithm design categories brute force method, Divide and Conquer, Dynamic programming, greedy approach, and backtracking.

3. Classification by Problem TypesBased on problem types or domain, the algorithm can be classified as follows:

Sorting Algorithms
Searching Algorithms
String Algorithms
Graph Algorithms
Combinatorial Algorithms
Geometric Algorithms

4. Classification based on Tractability

Based on tractability, the algorithms can be categorized as polynomial algorithms and Non- deterministic polynomial problems. Easy solvable problems are called polynomial algorithms and the problems for which solution is not possible or difficult to solve given the limited nature of resources are called NP algorithms.

This module can be concluded as follows:

Problem solving stages are problem understanding, planning, design, analysis, implementation and post-analysis.
Problem understanding and planning is important. Algorithm design and analysis is crucial.
Classification of Algorithms is based on implementation, design, problem type and tractability.
S.Sridhar – Design and Analysis of Algorithms , Oxford University Press, 2014.
Cormen, T.H., C.E. Leiserson, and R.L. Rivest, Introduction to Algorithms, MIT Press, Cambridge, MA 1992.

Python Programming
C Programming
Numerical Methods
Dart Language
Computer Basics
Deep Learning
C Programming Examples
Python Programming Examples

Problem Solving Using Computer (Steps)

Computer based problem solving is a systematic process of designing, implementing and using programming tools during the problem solving stage. This method enables the computer system to be more intuitive with human logic than machine logic. Final outcome of this process is software tools which is dedicated to solve the problem under consideration. Software is just a collection of computer programs and programs are a set of instructions which guides computer’s hardware. These instructions need to be well specified for solving the problem. After its creation, the software should be error free and well documented. Software development is the process of creating such software, which satisfies end user’s requirements and needs.

The following six steps must be followed to solve a problem using computer.

Problem Analysis
Program Design - Algorithm, Flowchart and Pseudocode
Compilation and Execution
Debugging and Testing
Program Documentation

IMAGES

Six steps problem-solving process infographic. Stock Vector
Master the 7-Step Problem-Solving Process for Better Decision-Making
Introdução aos Algoritmos
Effective Problem Solving in 5 Simple Steps by Synergogy
9 Step Problem Solving Model
Algorithmic Problem Solving

COMMENTS

2. FUNDAMENTALS OF ALGORITHMIC PROBLEM SOLVING - RCET
FIGURE 1.2.1 Algorithm design and analysis process. (i) Understanding the Problem • This is the first step in designing of algorithm. • Read the problem’s description carefully to understand the problem statement completely. • Ask questions for clarifying the doubts about the problem. • Identify the problem types and use existing ...
How to Use Algorithms to Solve Problems? - GeeksforGeeks
Aug 9, 2021 · Step 9: Again wait for some time until the sugar is melted. Step 10: Turn off the gas burner and serve the tea in cups with biscuits. Step 11: End. Here is an algorithm for making a cup of tea. This is the same for computer science problems. There are some basics steps to make an algorithm: Start – Start the algorithm
THE SIX-STEP PROBLEM-SOLVING PROCESS - ru
can be made?” in order for the solution to be effective, or work best on the problem. The Six-Step Problem-Solving Process is the most effective algorithmic process aimed at bettering how humans (mostly teenagers and students) handle and deal with arising problems. It works hand-in-hand with other useful methods such as the
Stucor CS8451-AA - Notes - 19. What are six steps processes ...
19. What are six steps processes in algorithmic problem solving? [Nov/Dec2009] - Understanding theproblem - Decision making on - Capabilities of computational devices, Choice of exact or approximate problem solving, Datastructures - Algorithmicstrategies - Specification ofalgorithm - Algorithmicverification - Analysis of algorithms
Fundamentals of Algorithmic Problem Solving - BrainKart
Do not skimp on this first step of the algorithmic problem-solving process; otherwise, you will run the risk of unnecessary rework. Ascertaining the Capabilities of the Computational Device. Once you completely understand a problem, you need to ascertain the capabilities of the computational device the algorithm is intended for.
The 6 Step Problem Solving Process - ru
There are many problem-solving methods, and the six-step method is just one of them.. •The problem for most people is that they do not use one process to solve problems and issues or simply just to make decisions. •People are not consistent in how they solve problems. •We do not find something that works and then do it the same way over and
16 Fundamental Stages of Problem Solving - INFLIBNET Centre
Fundamental Stages of Problem Solving . This module focuses on the stages of problem solving. The learning objectives of this module are as follows: To understand stages of Problem solving process; Characteristics of an Efficient Algorithm; To categorize algorithms; Fundamental stages of Problem Solving . Problem solving is both an art and science.
Problem Solving Using Computer (Steps) - Codesansar
Computer based problem solving is a systematic process of designing, implementing and using programming tools during the problem solving stage. This method enables the computer system to be more intuitive with human logic than machine logic. Final outcome of this process is software tools which is dedicated to solve the problem under consideration.
Chapter 3: Algorithmic Problem Solving
steps. An algorithm, whose characteristics will be discussed later, is a form that embeds the complete logic of the solution. Its formal written version is called a program, or code. Thus, algorithmic problem solving actually comes in two phases: derivation of an algorithm that solves the problem, and conversion of the algorithm into code.
Steps in Problem Solving — Computer Based Problem Solving 1.0 ...
The following is just one of many Six Step Problem Solving Systems, which can be used to solve any type of problem, not just ones that will be solved on a computer. The good thing is that the system translates nicely to computer problems, which is very useful, since the focus of the book is to solve problems on a computer.