experiment on young's modulus

Talk to our experts

1800-120-456-456

CBSE Physics Experiment Young’s Modulus of a Wire Using Searle’s Apparatus

Physics Experiment – Young’s Modulus of a Wire Using Searle’s Apparatus

With time, the perpetual need for the construction of more buildings, dams and bridges is increasing. For these industrial architects to become strong and durable, it is essential to have good knowledge of the modulus of elasticity of the material used for construction, i.e. the Young’s modulus, which we will study here.

Young’s modulus (Y) is defined as the ratio of tensile or compressive stress \[\sigma \] to the longitudinal strain \[\varepsilon \]:

\[Y = \dfrac{\sigma }{\varepsilon }\]

In this experiment, we are going to determine Young’s modulus Y of the material of a given wire using Searle’s apparatus , by determining the change in length of the wire under a constant weight using a screw gauge.

Table of Contents

Observations.

To determine Young’s modulus of the material of a given wire by Searle’s apparatus .

Apparatus required

Searle apparatus

Meter scale

Small weights

Screw gauge

Spirit level

The arrangement consists of two frames that are allowed to move vertically relative to each other, joined by a spirit level. One of the frames holds a reference wire and the other one the experimental wire, which is connected to a screw gauge. Both the frames contain hooks for hanging weights to taut. Due to the additional weights, the experimental wire suffers a small length elongation, which disturbs the spirit level bubble. The screw gauge is used to adjust the bubble again at its middle position and hence gives the reading of the elongation.

The apparatus works on the principle of Hooke’s law . The Young’s modulus Y of the wire is given by:

\[Y = \dfrac{{MgL}}{{\pi {r^2}\Delta L}}\]

where M = Mass of the hanged weights

L = Original length of the wire

r = Radius of the wire

\[\Delta L\]= Extension in length of wire

g = Acceleration due to gravity

Suspend small equal weights from both the wires to make them perfectly taut. Measure the length of each wire using a meter scale.

Determine the least count and zero error of the screw gauge. Determine the thickness of the given wire using a screw gauge at five different points on the wire. At each point, measure the thickness along two mutually perpendicular directions along its diameter and find the mean of the two. Divide it by 2 to get the radius.

Adjust the screw gauge such that the spirit level placed on the cross bar shows perfectly horizontal balance. Note the micrometer reading.

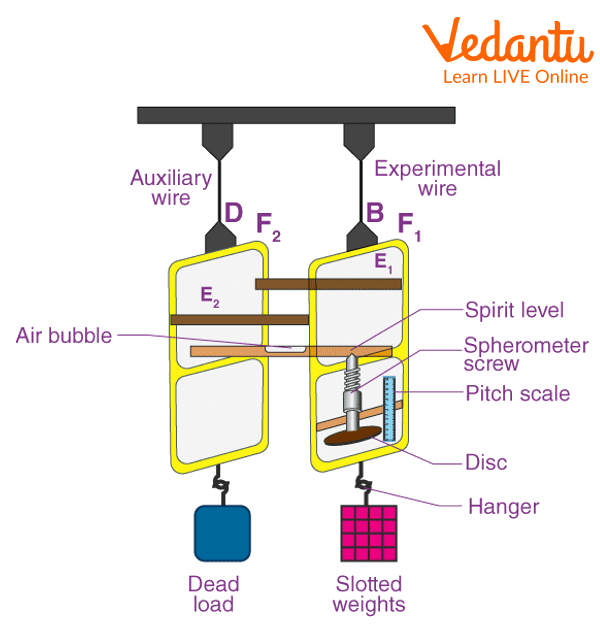
Searle’s Apparatus

Hang a weight of 0.5 kg to the given wire. The bubble in the spirit level will move away from the equilibrium position by a little bit. Adjust the screw gauge so as to bring it back to its equilibrium position. Note the reading in the screw gauge.

Increase the weight in steps of 0.5 kg and note the screw gauge reading in each case after using it to restore the position of the spirit level bubble.

Tabulate about 8 observations.

Length of the wire L = 

Least count (LC) of the screw gauge = 

Zero error of screw gauge = 

Observation Table – For the radius of wire

MSR = Main scale reading of screw gauge

CSD = Circular scale division coinciding of screw gauge

Mean diameter after correcting zero error = 

Mean radius = 

Observation Table – For the Extension of Wire

Observation table – mean extension in wire per 2 kg load.

Therefore, \[mean\;\Delta L = \dfrac{{(e - a) + (f - b) + (g - c) + (h - d)}}{4}\;cm\; = \;............\;cm\] for 2 kg

Young’s modulus of the material of wire,

\[Y = \dfrac{{MgL}}{{\pi {r^2}\Delta L}} = ...........\;N{m^{ - 2}}\]

Precautions

Both wires should be taut and uniform at all points.

Measure the thickness of wires very carefully at both orthogonal positions on the same point.

Determine the zero and backlash errors of the screw gauge very carefully.

Lab Manual Questions

1. State elastic limit of a material and Hooke’s law.

Ans: The maximum applied stress allowed on a material up to the limit so as not to cause permanent deformation in it is known as the elastic limit of that material. Within this limit, the strain developed inside the material is directly proportional to the stress applied on it. This law is known as Hooke’s law .

2. Explain Young’s modulus of a material.

Ans: Young’s modulus of a material is defined as the ratio of tensile or compressive stress applied to a material to the longitudinal strain produced in that material. Its SI unit is \[N{m^{ - 2}}\].

3. On what factors does the Young’s modulus of a material depend?

Ans: Young’s modulus of a material is given by the formula

It depends on the length L of the material, weight Mg used for deformation, its cross-sectional area \[\pi {r^2}\] and the amount of length deformation \[\Delta L\]. The value of Young’s modulus is constant for a given material but depends on external parameters such as temperature and pressure.

4. What is the rigidity modulus of a material?

Ans: Modulus of rigidity is defined as the ratio of shearing stress applied on a material to the shearing strain produced in that material. It is also known as shear modulus .

Viva Questions

1. Why does an elongation in a metallic rod hinged at one end in this experiment?

Ans: When the load is applied on the wire, the wire stretches by a small amount due to it. This strains the wire and hence the wire elongates.

2. In Young’s modulus experiment, why do we use two wires?

Ans: In Young’s modulus experiment, we use one reference wire and an experimental wire. The reference wire measures the small but finite elongation in the experimental wire due to applied load using a screw gauge.

3. Is it possible to determine the rigidity modulus of gases?

Ans: No, it is not simply possible to determine the rigidity modulus of gases because one cannot apply shearing stress on them due to large inter-particle separation and cannot measure their shearing strain.

4. In the above experiment, how do stress and strain get produced in the material?

Ans: In the above experiment, the stress is applied to the experimental wire by virtue of slotted weights, and the strain is produced in it in response due to stress applied in the form of longitudinal elongation of the wire.

5. What is Young’s modulus of elasticity?

Ans: Young’s modulus of elasticity is defined as the ratio of tensile stress to the longitudinal strain of material.

6. Give Young’s modulus formula.

Ans: The Young’s modulus Y of a material is given by:

where F = Force applied on the material

A = Cross sectional area of the material

\[\Delta L\]= Length extension in the material

L = Given length of the material

7. If an elastic material with Young’s modulus Y is subjected to stretching stress S, obtain the expression for elastic energy stored per unit volume in the material.

Ans: Energy stored per unit volume = \[\dfrac{1}{2} \times Stress \times Strain\]

Since Young’s modulus \[Y = \dfrac{{Stress}}{{Strain}} = \dfrac{S}{{Strain}}\;\;\;\;\; \to \;\;\;\;\;Strain = \dfrac{S}{Y}\]

Therefore, energy stored per unit volume = \[\dfrac{1}{2} \times S \times \dfrac{S}{Y} = \dfrac{{{S^2}}}{{2Y}}\]

8. Define elastic deformation.

Ans: The deformation caused on an elastic body due to external deforming force before the body regains its initial shape and size is known as elastic deformation .

9. What is the shear modulus?

Ans: The ratio of shearing stress to the corresponding shearing strain of a material is known as the shear modulus of that material.

10.  Give three useful examples of elasticity in Physics.

Ans: Useful examples of elasticity in physics include rubber bands , springs and trampoline .

Practical Questions

1. What is the modulus of rigidity of ideal liquids?

Ans: (A) Zero

Since modulus of rigidity is a measure of rigidity of the body and ideal liquids are incompressible, non-viscous and have infinite shear strain, therefore the modulus of rigidity of ideal liquids is zero .

2. Choose the incorrect statement among the following:

Modulus of elasticity is a direct measure of the elasticity of the material

Elasticity of a material is inversely proportional to temperature

Modulus of rigidity of a material is directly proportional to temperature

For ideal fluids, bulk modulus is infinite

Ans: (C) 

Modulus of rigidity of a material is independent of temperature .

3. Hooke’s law specifies:

Modulus of elasticity

Elastic limit

Ans: (C) Hooke’s law specifies the modulus of elasticity as the ratio of stress to strain within the elastic limit.

4. On which factor does the breaking stress of a wire depend?

Material of wire

Length of wire

Thickness of wire

Shape of cross-section of wire

Ans: (A) The breaking stress of a wire depends upon the material of the wire.

5. The stress at which an elastic material transforms into a plastic material is known as:

Normal stress

Ultimate stress

Thermal stress

Yield strength

Ans: (D) The stress at which an elastic material transforms into a plastic material is known as yield strength .

6. How do the elastic properties of gold change when it is electroplated with another metal?

Remain unaffected

Ans: (C) When gold is being electroplated with another metal, its elastic properties increase due to an increase in impurity concentration .

7. How does hammering affect the elasticity of materials?

Has no effect

Elasticity increases

Elasticity decreases

Material loses its elasticity

Ans: (B) Hammering breaks down the material into smaller units that resist the deformation more effectively. Hence, elasticity increases .

8. Why does a bridge collapse when it experiences a heavy load?

Due to weak structure

Due to increase in stress

Due to faulty materials for construction

Due to friction

Ans: (A) Due to increase in stress (force per unit area)

9. What is the effect of annealing on elasticity?

Elasticity remains same

Elasticity increases in some regions and decreases in others

Ans: (A) Annealing results in forming larger material crystals which resist deformation less effectively. Hence, elasticity decreases .

10. What should be done to prevent the breaking of rope under a large force?

Length should be increased

Small force should be applied

Rope’s cross sectional area should be increased

Rope made of a different material should be used

Ans: (C) Upon increasing the cross sectional area of the rope, the stress experienced by it decreases due to inverse proportionality .

From this experiment, we can conclude that elasticity plays a crucial role in physics and engineering. Good knowledge of the elasticity of various materials plays a very important role in the construction of houses, buildings, dams and much more. It also plays a significant role in our daily lives in the form of rubber bands , trampolines , springs etc.

We hope that the reader has got a good insight into the topic through this experiment and is encouraged to explore the relevant topics in Physics.

FAQs on CBSE Physics Experiment Young’s Modulus of a Wire Using Searle’s Apparatus

1. What is strain energy?

Strain energy is defined as the energy stored in a body due to deformation in its shape and size.

2. What is resilience modulus?

When a material is stressed to its elastic limit, the maximum mechanical energy stored per unit volume in the material is known as the modulus of resilience.

3. What is the property of brittleness?

Brittleness is the property of materials in which they break down without deformation. Their fracture point comes very early without warning.

4. State the three types of moduli of elasticity.

The three moduli of elasticity are:

Young’s modulus

Bulk modulus

Shear modulus

5. What is Poisson’s ratio?

Poisson’s ratio is the ratio of lateral strain in a wire to its longitudinal strain within the elastic limit. Its normal value lies between -1 and \[\dfrac{1}{2}\] and practical value lies between 0 and \[\dfrac{1}{2}\].

Dissemination of IT for the Promotion of Materials Science (DoITPoMS)

Experiment: Measurement of Young's modulus

View a definition of Young's Modulus .

A cantilever beam is fixed at one end and free to move vertically at the other, as shown in the diagram below.

Geometry of the cantilever beam test.

For each of three strips of material (steel, aluminium and polycarbonate), the strip is clamped at one end so that it extends horizontally, with the plane of the strip parallel to the plane of the bench. A small weight is hung on the free end and the vertical displacement, δ , measured. The value of δ is related to the applied load, P , and the Young’s Modulus, E , by

where L is the length of the strip, and I the second moment of area (moment of inertia). View derivation of equation .

For a prismatic beam with a rectangular section (depth h and width w ), the value of I is given by

By hanging several different weights on the ends of the strips, and measuring the corresponding deflections, a graph can be can be plotted which allows the Young's modulus to be calculated. This is repeated for each of the three materials. The calculated values for the Young’s modulus may be compared with the values in this properties table .

Your browser does not support the video tag.

Experiment to determine Young's modulus

Measuring Young's modulus. (Click on image to view a larger version.)

View QuickTime video of experiment (1.2 MB) ... in separate window ... video alone .

Help with viewing video clips

Cyberphysics - a web-based teaching aid - for students of physics, their teachers and parents....

A-Level Physics

Physics A-Level Resources for AQA, OCR and Edexcel

Young’s Modulus

Introduction

Young’s modulus is a numerical constant, named after the 18th-century English physician and physicist Thomas Young. Young’s modulus is a measure of the ability of a material to withstand changes in length under lengthwise tension or compression. Young’s modulus is also termed the modulus of elasticity.

A. Young’s modulus

Most materials under small strain obey Hooke’s law. Under this circumstance, the ratio between stress and strain is constant. This quantity is called Young’s modulus (E). Young’s modulus measures the resistance of a material to elastic deformation.

B. What Young’s Modulus Means

Young’s modulus describes the stiffness of a material. In simpler terms, it states how easy it is to bend or stretch the material. Young’s modulus of a material is its fundamental property that remains unchanged. But, it is dependent on material temperature. The stress-strain graph for two materials is illustrated in Figure 1 . Material A is stiffer than material B, as a higher stress is needed to produce the same amount of strain. So, Material A will have higher Young’s modulus than Material B.

Figure 1: Young’s Modulus Comparison

C. How to Calculate Young’s Modulus

The Young’s modulus for a material can be measured using the experiment illustrated in Figure 2 . The reference wire and test wire made of the selected material are hung from the ceiling. The reference wire supports a vernier scale, which will measure the extension of the test wire. The slotted masses can be used to vary the force acting on the test wire.

Figure 2: Experiment Set-up

D. Applications of Young’s Modulus

Young’s modulus is very important for doctors and scientists. This parameter can help them determine when a structural implant will deform. Hence, they can design a piece mechanically for use in the body. The following table shows Young’s modulus for different values and applications of the materials.

An Example of Application

A steel wire of diameter 4.0 mm (Area = 12.5 x 10^(-6) m^2) and length 30 m is suspended from an overhead crane and a load of 1500 N is suspended from its free end. The Young’s modulus of the material of the wire is 210 x 10^9 N. It is assumed that the proportionality limit of the wire is not exceeded. The stress, strain and the extension of the wire used in the overhead crane are calculated.

Young’s modulus is an important material property because of its relationship with stress and strain. Young’s modulus for almost all materials is established. In several engineering design calculations, Young’s modulus is used to find either thickness of the material to withstand a given load or stress level on the material for a given load.