guess and check problem solving

Fun teaching resources & tips to help you teach math with confidence

Math Strategies: Solving Problems Using Guess and Check

Welcome to the last post in my series on problem solving strategies ! There are so many different ways to approach math word problems, but it’s important that we share these various methods with kids so that they can be equipped to tackle them. This week I’m explaining a strategy that doesn’t sound overly mathematical , but can be extremely useful when done properly: solving problems using guess and check ! As with the other strategies I’ve discussed, it’s important to help kids understand how to use this method so that they are not randomly pulling answers out of their head and wasting time .

–>Pssst! Do your kids need help making sense of and solving word problems? You might like this set of editable word problem solving templates ! Use these with any grade level, for any type of word problem :

Guess & Check Math Strategy: 

You may hear the name of this strategy and think, “Guess? Isn’t the whole point of math instruction to teach kids to solve problems so that they’re no longer merely guessing ??”

While it is certainly true that we don’t want kids to simply guess random answers for every math problem they ever encounter, there are instances when educated guesses are important, valid and useful.

For instance, learning and understanding how to accurately estimate is an important mathematical skill. A good estimate, however, is not just a random guess. It takes effort and logic to formulate an estimate that makes sense and is (hopefully) close to the correct answer. (For fun and easy estimation practice, try this Mummy Math activity ! )

Similarly, solving problems using guess and check is a process that requires logic and an understanding of the question so that it can be done in a way that is organized and time saving.

So what does guess and check mean? To be more specific, this strategy should be called, “Guess, Check and Revise.”

The basic structure of the strategy looks like this:

• Form an educated guess
• Check your solution to see if it works and solves the problem
• If not, revise your guess based on whether it is too high or too low

This is a useful strategy when you’re given the total and you’re asked to find the kinds or number of things making up the total.

Or when the question asks for the value of two or more different kinds of things .

For instance, you might be asked how many girls and how many boys are in the class, or how many cats and how many dogs a pet owner has.

When guess and check seems like an appropriate strategy for a word problem, it will be helpful and necessary to then organize the information in a table or list to keep track of the different guesses.

This provides a visual of the important information, and will also help ensure that subsequent guesses are logical and not random .

Using the Guess and Check Strategy:

To begin, students should make a guess using what they know from the problem. This first guess can be anything at all, so long as it follows the criteria given. Then, once a guess is made, students can begin to make more educated guesses based on how close they are to the correct answer.

For example, if their initial guess gives a total that is too high, they need to choose smaller numbers for their next guess.

Likewise, if their guess gives a total that is too low, they need to choose larger numbers.

The most important thing for students to understand when using this method is that after their initial guess, they should work towards getting closer to the correct answer by making logical changes to their guess. They should not be choosing random numbers anymore!

Here’s an example to consider:

In Ms. Brown’s class, there are 24 students. There are 6 more girls than boys. How many boys and girls are there?

Because we know the class total (24), and we’re asked to find more than one value (number of boys and number of girls), we can solve this using the guess and check method .

To organize the question, we can form a table with boys, girls and the total. Because we know there are 6 more girls than boys, we can guess a number for the boys, and then calculate the girls and the total from there.

With an initial guess of 12 boys, we see that there would be 18 girls, giving a total class size of 30. The total, however, should only be 24, which means our guess was too high . Knowing this, the number of boys is revised and the total recalculated .

Lowering the number of boys to 10 would mean there are 16 girls, which gives a class total of 26. This is still just a little bit too high, so we can once again revise the guess to 9 boys. If there are 9 boys, that would mean there are 15 girls, which gives a class total of 24.

Therefore, the solution is 9 boys and 15 girls.

This is a fairly simple example, and likely you will have students who can solve this problem without writing out a table and forming multiple guesses. But for students who struggle with math , this problem may seem overwhelming and complicated.

By giving them a starting point and helping them learn to make more educated guesses , you can equip them to not only solve word problems, but feel more confident in tackling them.

This is also a good strategy because it helps kids see that it’s ok to make mistakes and that we shouldn’t expect to get the right answer on the first try, but rather, we should expect to make mistakes and use our mistake to learn and find the right answer.

What do you think? Do you use or teach this strategy to students? Do you find it helpful?

And of course, don’t miss the rest of the problem solving strategy series:

• Problem Solve by Solving an Easier Problem
• Problem Solve by Drawing a Picture
• Problem Solve by Working Backwards
• Problem Solve by Making a List
• Problem Solve by Finding a Pattern

My strategy was usually more “guess and hope for the best”. Yours sounds much wiser, lol! Thanks for sharing at the Thoughtful Spot!

Haha!! Yes, I think that’s what most people think of when they hear, “Guess and Check!” Hope this was helpful, 🙂

How exactly do you do this?

Sorry, your way was amazing…but I’m still confused:(

I’m so sorry you’re confused. Can you explain what part you don’t understand so I can try and make it clearer? The object is to make a reasonable guess, and then adjust your guess based on if your answer is too high or too low (try to be logical rather than random).

Nicely explained post and a different logic for solving problems “Guess and check”, I don’t know that how much helpful it is but I’m sure that your idea will help to change the thinking of readers. Thanks for sharing a different kind of idea for problem solving.

Comments are closed.

Similar Posts

Weekly Math Freebie Round Up!

All about constellations {easy craft and science lesson}.

Adding & Subtracting Decimals Partner Challenge {FREE!}

Sidewalk Chalk Jumping Maze Math Challenge

The 20+ Best Math Card Games That Are Easy To Learn

Symmetry for Kids: 20+ Ideas & Resources

Find more resources to help make math engaging, join 165k+ parents & teachers.

Who learn new tips and strategies, as well as receive engaging resources to make math fun!

• Privacy Policy

Math Time Doesn't Have to End in Tears

Join 165,000+ parents and teachers who learn new tips and strategies, as well as receive engaging resources to make math fun. Plus, receive my guide, "5 Games You Can Play Today to Make Math Fun," as my free gift to get you started!

Math Problem Solving: The Guess and Check Method

Teach students the same technique research mathematicians use! (Seriously.)

Need more tips and tricks for teaching math? You can find them in our math resources center .

In this article, we will explore the guess and check method, a powerful yet simple problem-solving strategy used in mathematics. We’ll guide you on how to teach this method effectively, using concrete examples and a step-by-step approach. 

What is the Guess and Check Method?

The guess and check method is a problem-solving strategy that students can use to solve  mathematical  problems. This strategy involves guessing the answer and then checking that the guess fits the conditions of the problem.

For example: 

The following problem would be best solved using the guess and check method:

Of 25 rounds at the regional spelling contest, the Mighty Brains tied 3 rounds and won 2 more than they lost. How many rounds did the Mighty Brains win?

Why Is This Strategy Important?

All research mathematicians use guess and check, and it is one of the most powerful methods of solving differential equations, which are equations involving an unknown function and its derivatives.

A mathematician's guess is called a "conjecture" and looking back to check the answer and prove that it is valid, is called a "proof." The main difference between problem-solving in the classroom and mathematical research is that in school, there is usually a known solution to the problem. In research, the solution is often unknown, so checking solutions is a critical part of the process.

When to Use the Guess and Check Method?

The guess and check method is particularly useful when a word problem  provides the value of both items, a total quantity, and the total value.

It is also a useful method when there is a limited set of possibilities that can be easily enumerated and checked.

Finally, it’s a handy method when the mathematical problem doesn't lend itself to other strategies. It is a good way to begin understanding the problem at hand.

How to Teach the Guess and Check Method

For this section, we will help you understand how to teach students to use the guess and check method using the following word problem as an example:

Ben knows 100 baseball players by name. Ten are Red Sox. The rest are Blue Jays and Diamondbacks. He knows the names of twice as many Diamondbacks as Blue Jays. How many Blue Jays does he know by name?

1. Ensure students understand the problem

The first step to solving a word problem like the one above is to make sure you understand what is being asked. Demonstrate to students that understanding is the first step.

Understanding the problem involves finding key pieces of information needed for finding the answer. This may require reading the problem several times, and/or having students put the problem into their own words.

Example: "I know there are twice as many Diamondbacks as Blue Jays. There are 10 Red Sox. The number of Blue Jays and Diamondbacks should equal 90.”

2. Choose a strategy

For this problem, we will be using the guess and check method.

Guess and check is often one of the first strategies that students learn when solving problems. This is a flexible strategy that is often used as a starting point when solving a problem, and can be used as a safety net, when no other strategy is immediately obvious.

3. Use a table to chart your guesses

Now, solve the problem. You may want to set up a table to record the guesses.

Guess a greater number of Blue Jays.

Now guess a greater number of Blue Jays.

Now guess a number lesser than 40 and greater than 20.

That is the answer.

4. Check over your work

After your students find the answer, remind them to check over their work.

Read the problem again to be sure the question was answered.

Yes, I found the number of Blue Jays.

Check the math to be sure it is correct.

30 doubled is 60. 30 + 60 + 10 = 100

Determine if the best strategy was chosen for this problem, or if there was another way to solve the problem.

Guess and check was a good way to solve this problem.

5. Explain your work

The last step is explaining how the student found the answer. Demonstrate how to write a paragraph describing the steps and how decisions were made throughout the process. Have students justify their answers.

6. Guided Practice

Have students try solving this problem using the strategy of Guess and Check.

Have students work in pairs, groups, or individually to solve this problem. They should be able to tell or write about how they found the answer and justify their reasoning.

Stretch this Strategy

The guess and check method can be made more sophisticated by improving each guess based on the last guess. Encourage students to analyze their guesses to determine what the next guess should be. Students can use patterns in the problem or in their guesses to determine the correct guess.

Students may not want to use any other strategy once they have learned guess and check, because it is so easy to use. When children are completely stuck, guessing and checking provides a useful place to start, but may not be the most efficient strategy. As problems get more difficult, other strategies become more important and more effective, but by starting with guess and check, the students may find a more efficient strategy that leads to a solution.

The full page is available ONLY to subscribers. Sign up today to get access to this page and all of the content on TeacherVision®.

Featured High School Resources

TEACHING RESOURCE

Writing Differentiation Strategies and Activities for High School

Close learning gaps this Fall with differentiated writing instruction This resource provides 5 strategies and 2 editabl...

Reading Differentiation Strategies and Activities for High School

Close learning gaps this Fall with differentiated reading instruction This resource provides 5 strategies and 3 editabl...

Math Differentiation and Remediation Strategies for High School

Close learning gaps with differentiated and remediated math instruction This resource provides 5 strategies for how to ...

Related Resources

Problem solving: draw a picture.

Problem Solving: Draw a Picture What Is It? The draw a picture strategy is a problem-solving technique in which students...

Problem Solving: Choose the Operation

Problem Solving: Choose the Operation What Is It? The process of "choosing the operation" involves deciding which mathem...

Problem Solving: Simplify the Problem

Problem Solving: Simplify the Problem What Is It? Simplifying a mathematics problem is a strategy that often is used alo...

Estimating Unknown Quantities

Estimating Unknown Quantities What Is It? Estimation is the process of guessing the approximate value of a number.

Theory and Evidence

Theory and Evidence What Is It? The terms theory and evidence go hand in hand.

Teaching Mathematics to Gifted Students in a Mixed-Ability Classroom

From: The ERIC Clearinghouse on Disabilities and Gifted Education ERIC EC Digest #E594Author: Dana T.

About the author

Haley Horton

Digital content manager & editor, about haley.

Learn the Guess and Check Method

What is the guess and check math strategy.

The Guess and Check Math strategy is one of the first few Math Heuristics that is introduced to Primary 3 students. Although some students may switch to more advanced techniques like the Assumption method in Primary 4, mastering this method is still going to be useful to those who don’t in their upper primary years. The main idea behind the Guess and Check method is to guess the answer to a problem and then check if the answer fits the given scenario. If it doesn’t, we’ll adjust our guess accordingly until all conditions are met.

Here’s what we’re going to cover:

• How does the Guess and check method work
• Examples of guess and check questions
• How to identify guess and check questions
• How to part 1: Building the guess and check table
• How to part 2: How to do the guess and check method

How does the Guess and Check Method work?

The Guess and Check problem solving strategy is a fairly easy way of solving problems. Think of it as a 3-step-approach:

1. Guess –> 2. Check –> 3. Repeat if needed

While we are guessing the numbers, we’ll need to learn how to make smart guesses. Knowing how to do that helps us minimize the number of guessing, making the process more efficient. We’ll see how to do that in a while.

Back to top

Examples of Guess and Check Questions

Here are some samples of how Guess and Check Math Questions can look like. Can you figure out what they have in common?

Primary 3 and 4 Math:

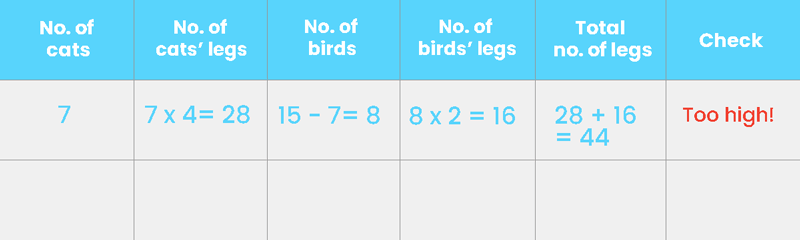
There are 15 cats and birds in a park. There are 42 legs altogether.

How many cats are there?

Primary 5 and 6 Math: Jay did 20 Math questions during his math practice. He received 5 marks for every correct answer and he got 2 marks deducted for every wrong answer. If Jay earned 35 experience points in total, how many questions did he answer wrongly?

How do we identify questions that use the Guess and Check Method?

If you looked carefully, both problems that you see above has a total that’s made up of 2 kinds of items. on top of that, we also have some information about each item and we need to find the number of one of those items. Let’s use the lower primary math problem as an example and go through the Guess and Check method step by step.

Part A: How to build the Guess and Check table the right way

Before we start guessing and checking, it’s always a good habit to build a guess and check table so that we know exactly what to look out for and keep things organised.

Step 1: List the 2 items that is in the question

The first thing that we’ll want to do is to build our guess and check table is to think about what we want to solve for. This is the answer that we are going to guess and it goes into our first column. In our case, it’s going to be the number of cats. Next, we’ll list the number of the second item, which happens to be the number of birds as shown below:

Step 2: List the common thing that the 2 items have

What do the cats and birds have in common? Legs. So the number of cats’ legs and the number of birds’ legs go into another 2 columns.

Step 3: Add in what we need to check 

Time to think about the relationship between the columns and how they help us check if the answer that we have guessed is correct. For our answer to be right, the total number of legs that we have has to add up to 42 and the way that we calculate this is to add the number of cats’ legs to the number of birds’ legs. Let’s add another column to include the total number of legs and because we are going to use this to check of our guess is correct, we are going to add in another special column called “Check” to help us keep track of our progress.

Is the Guess and Check Table really necessary?

When we are busy making guesses, it is easy to lose track of the numbers that we have tried along with their calculations. That’s where a guess and check table can really come in handy. Not only does a guess and check table help us organize our guesses in a neat visual way, it also prevents us from making careless mistakes.

How to use the Guess and Check method efficiently

As you might have guessed, guessing and checking comes with a lot of hits and misses. Here’s the trick to keep our guesses to a minimal and make the guess and check method work better!

Step 1: Start with the middle number as your first guess

In our example, since we have 15 pets,  half of 15 would be approximately 7 or 8 (not 7.5 because we can’t have half a pet). Let’s pick 7 as our guess.

Step 2: Filling up our guess and check table from left to right

Once we have our guess, it’s time to work through the columns of our guess and check table and decide if our guess is correct. If we had 7 cats and each puppy has 4 legs, we are going to have 7 x 4 cats’ legs = 28 cats’ legs. To find the number of birds, let’s subtract 7 from the total of 15 pets. This gives us 8 birds. 8 birds are going to have 8 x 2 birds’ legs, 16 legs in all. Let’s check the total number of legs we have against what is given in the problem. When we add 28 and 16, we are going to get a total of 44 legs. However, this is more than the 42 legs that we are given in the problem. Let’s make a note of that under the “Check” column.

Step 3: Adjust our guess accordingly and check again

The next thing that we’ll want to do is to estimate how far our guess is to our target, and make a better guess. Comparing our guess which resulted in 44 legs against the 42 legs that we want, we can tell that our guess is very close. Since we want to reduce the number of legs, should we increase or decrease our second guess? Because the cats have more legs than birds and we want fewer legs, we’ll need to lower what we’ve guessed. When we work systematically across our guess and check table, this happens to be the answer that we are looking for!

All it takes for us to get the correct answer are 2 guesses, and this definitely didn’t happen by chance. When we made the first guess, it gave us some information about how far we are from the answer. This helped us make a better guess the second time. As you can see, we are making logical guesses instead of just guessing random numbers and trying our luck.

And that’s how you do the Guess and Check method!

Using the Guess and Check method is good when you are dealing with smaller numbers which are easier to work with. However, it does take practice to improve the accuracy of your guesses and some children may take a longer time to do the calculations in between, giving room to possible careless mistakes. If you are looking for a faster alternative that involves fewer steps, you might want to check out the Assumption Method and see if that works better for you.

Need more examples?

Check out how this Math video on how to use the guess and check method to solve a Primary 3 question.

Like what you see? Subscribe to our Youtube channel for more Practicle Singapore Math videos!

Practicle is an online gamified Singapore Math adaptive learning platform that helps primary school children master Math through understanding and fun.

• EAF Certification
• Privacy policy
• Terms of use
• Math heuristics guide
• Math problem sum guide

© 2024 Practicle. All Rights Reserved,

• A.I. Math Tutor
• Math Vision: Our video tutorials

Shopping Cart

No products in the basket.

Guess-and-Check Method for Guess & Check Questions: Example

Math heuristics for problem solving, primary 3 guess-and-check & its method, what is guess-and-check in math.

The Guess-and-Check method is a problem-solving strategy used in math to find a solution by making an initial guess and checking whether it is correct or not . If the guess is incorrect, a new guess is made and checked until the correct answer is found . This method can be used when there is no obvious formula or method to solve the problem, and is particularly useful when dealing with word problems. It can be time-consuming, but can also be a useful way to develop problem-solving skills and intuition.

Guess-and-Check is useful when a word problem provides the values of both items, the total quantity, and the total value . In such cases, both the Assumption or Guess-and-Check method can help find the solution.

How to Solve Math Questions with Guess-and-Check Method?

Let's take a look at this primary 3 word problem example:.

Watch the tutorial for free!

Ronald bought 8 pens and rulers for $21. Each pen cost $3 and each ruler cost $2. How many pens did Ronald buy?

Identify the Concept

The question has 2 values and 2 totals, the total quantity and the total value. Both Guess-and-Check and Assumption methods can works for this scenario.

Workings Explained

• The Total Quantity → 8 pens and rulers
• The Total Value → $21 (The total amount Ronald paid for all the pens and rulers)
• 2 Values → 1 Pen cost $3, 1 Ruler cost $2.

For Guess and Check , we can actually start with any number as long as the total quantity adds up to the total quantity that was provided. Most teachers will advise their pupils to start with half-half (half of each item).

Note: For Guess & Check method, there must at least 3 guess.

• 4 rulers cost: 4 (rulers) × 2 (cost of 1 ruler) = 8
• 4 pens cost: 4 (pens) × 3 (cost of 1 pen) = 12.
• Total value: 8 + 12 = 20

✗ Wrong guess

• 5 rulers cost: 5 (rulers) × 2 (cost of 1 ruler) = 10
• 3 pens cost: 3 (pens) × 3 (cost of 1 pen) = 9.
• Total value: 10 + 9 = 19
• 3 rulers cost: 3 (rulers) × 2 (cost of 1 ruler) = 6
• 5 pens cost: 5 (pens) × 3 (cost of 1 pen) = 15.
• Total value: 6 + 15 = 21

✓ Correct guess

See other problem-solving strategies and methods

Watch 13 Math Problem-Solving Lessons for Free!

Simply sign up for Basic Access to get started.

What's Problem Sum?

Problem Sum is a term commonly used in the context of math education, particularly in regions that follow the Singapore Math curriculum . It refers to a type of math problem that typically involves multiple steps and requires students to apply various mathematical concepts and strategies to find the solution. These problems are often word problems that describe a real-world scenario, requiring students to read, comprehend, and analyze the situation before applying the appropriate math operations to solve it.

In essence, a Problem Sum combines elements of arithmetic and logical reasoning , challenging students to think critically and use their problem-solving skills. It is a key component in developing a deeper understanding of math concepts and enhancing analytical abilities in students.