case study of phylogenetic analysis

Loading metrics

Open Access

Peer-reviewed

Research Article

Unifying approaches from statistical genetics and phylogenetics for mapping phenotypes in structured populations

Roles Conceptualization, Formal analysis, Investigation, Methodology, Visualization, Writing – original draft, Writing – review & editing

Affiliation Department of Quantitative and Computational Biology, University of Southern California, Los Angeles, California, United States of America

Contributed equally to this work with: Michael D. Edge, Matt Pennell

Roles Conceptualization, Formal analysis, Funding acquisition, Investigation, Methodology, Writing – original draft, Writing – review & editing

* E-mail: [email protected] (MDE); [email protected] (MP)

Affiliations Department of Quantitative and Computational Biology, University of Southern California, Los Angeles, California, United States of America, Department of Biological Sciences, University of Southern California, Los Angeles, California, United States of America

• Joshua G. Schraiber, 
• Michael D. Edge, 
• Matt Pennell

• Published: October 9, 2024
• https://doi.org/10.1371/journal.pbio.3002847
• Reader Comments

In both statistical genetics and phylogenetics, a major goal is to identify correlations between genetic loci or other aspects of the phenotype or environment and a focal trait. In these 2 fields, there are sophisticated but disparate statistical traditions aimed at these tasks. The disconnect between their respective approaches is becoming untenable as questions in medicine, conservation biology, and evolutionary biology increasingly rely on integrating data from within and among species, and once-clear conceptual divisions are becoming increasingly blurred. To help bridge this divide, we lay out a general model describing the covariance between the genetic contributions to the quantitative phenotypes of different individuals. Taking this approach shows that standard models in both statistical genetics (e.g., genome-wide association studies; GWAS) and phylogenetic comparative biology (e.g., phylogenetic regression) can be interpreted as special cases of this more general quantitative-genetic model. The fact that these models share the same core architecture means that we can build a unified understanding of the strengths and limitations of different methods for controlling for genetic structure when testing for associations. We develop intuition for why and when spurious correlations may occur analytically and conduct population-genetic and phylogenetic simulations of quantitative traits. The structural similarity of problems in statistical genetics and phylogenetics enables us to take methodological advances from one field and apply them in the other. We demonstrate by showing how a standard GWAS technique—including both the genetic relatedness matrix (GRM) as well as its leading eigenvectors, corresponding to the principal components of the genotype matrix, in a regression model—can mitigate spurious correlations in phylogenetic analyses. As a case study, we re-examine an analysis testing for coevolution of expression levels between genes across a fungal phylogeny and show that including eigenvectors of the covariance matrix as covariates decreases the false positive rate while simultaneously increasing the true positive rate. More generally, this work provides a foundation for more integrative approaches for understanding the genetic architecture of phenotypes and how evolutionary processes shape it.

Citation: Schraiber JG, Edge MD, Pennell M (2024) Unifying approaches from statistical genetics and phylogenetics for mapping phenotypes in structured populations. PLoS Biol 22(10): e3002847. https://doi.org/10.1371/journal.pbio.3002847

Academic Editor: Leonie C. Moyle, Indiana University, UNITED STATES OF AMERICA

Received: March 7, 2024; Accepted: September 17, 2024; Published: October 9, 2024

Copyright: © 2024 Schraiber et al. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

Data Availability: A stable release of the code used to generate the results in this paper can be found at https://zenodo.org/doi/10.5281/zenodo.13738529 ; the associated GitHub repository can be found here https://github.com/Schraiber/PGLS_GWAS . All the simulation results and empirical data can be downloaded from https://zenodo.org/records/13774370 .

Funding: We acknowledge support from NIH grant R35GM137758 to MDE and R35GM151348 to MP. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Competing interests: The authors have declared that no competing interests exist.

Abbreviations: ARG, ancestral recombination graph; eGRM, expected genetic relatedness matrix; GLMM, generalized linear mixed model; GLS, generalized least squares; GRM, genetic relatedness matrix; GWAS, genome-wide association studies; LMM, linear mixed model; MSA, multiple sequence alignment; PCM, phylogenetic comparative method; PGLS, phylogenetic generalized least squares

1 Introduction

Statistical genetics and phylogenetic comparative biology share the goal of identifying correlations between features of individuals (or populations) that share ancestry. In the case of statistical genetics, researchers search for causal genetic variants underlying a phenotype of interest, whereas in phylogenetic comparative biology, researchers are typically interested in testing for associations among phenotypes or between a phenotype and an environmental variable. In both cases, these tests are designed to isolate the influence of a focal variable from that of many potential confounding variables. But despite the shared high-level goal, the statistical traditions in these 2 fields have developed largely separately, and—at least superficially—do not resemble each other. Moreover, researchers in these 2 statistical traditions may have different understandings of the nature of the problems they are trying to solve.

In statistical genetics, phenotypes and genotypes can be spuriously associated because of confounding due to population structure [ 1 – 4 ] or assortative mating [ 5 , 6 ]. For example, in their famous “chopsticks” thought experiment, Lander and Schork [ 1 ] pointed out that genetic variants that have drifted to higher frequency in subpopulations in which chopsticks are frequently used will appear, in a broad sample, to be associated with individual ability to use chopsticks, even though the association is due to cultural confounding and not to genetic causation. Confounding can also be genetic [ 7 ]—if a genetic variant that changes a phenotype is more common in one population than others, leading to differences in average phenotype among populations, then other, noncausal variants that have drifted to relatively high frequency in this population may appear to be associated with the phenotype in a broad sample. In addition to affecting genome-wide association study (GWAS) results, such confounding can affect heritability estimation [ 8 , 9 ], genetic correlation estimates [ 10 , 11 ], and prediction of phenotypes from polygenic scores [ 12 – 16 ]. Although many candidate solutions have been offered [ 17 – 21 ], the 2 most common approaches involve adjusting for shared ancestry using the genetic relatedness matrix (GRM, [ 22 ]), either by incorporating individual values on the first several eigenvectors of this matrix (i.e., the principal components of the genotype matrix) as fixed effects [ 23 ], or by modeling covariance among individuals attributable to genome-wide relatedness in a linear mixed model (LMM, [ 24 – 28 ]).

In phylogenetic comparative biology, researchers typically aim to control for the similarity of related species by incorporating the species tree into the analysis. There has been a great deal of controversy as to what the underlying goals and implicit assumptions of phylogenetic comparative methods (PCMs) are (see for examples refs. [ 29 – 36 ]). But broadly speaking, it seems that many researchers understand the goal of PCMs to be avoiding “phylogenetic pseudoreplication” [ 37 ]—mistaking similarity due to shared phylogenetic history for similarity due to independent evolutionary events [ 34 ]. This is most commonly done by conducting a standard regression, using either generalized least squares (GLSs) or a generalized linear mixed model (GLMM), but including the expected covariance structure owing to the phylogeny [ 38 – 42 ]. (Throughout this paper, we do not make a distinction between phylogenetic GLS and phylogenetic GLMM models. We refer to them generically by the shorthand GLS for the general case and PGLS for cases where the phylogenetic variance-covariance matrix is used.) This covariance structure reflects both the relatedness of species and the expected distribution of phenotypes under a model of phenotypic evolution [ 43 , 44 ], such as a Brownian motion [ 45 ] and related alternatives [ 44 ]. (The “phylogenetically independent contrasts” method [ 46 ], which ushered in modern PCMs, is statistically equivalent to a PGLS model assuming a Brownian model [ 47 ].)

In recent years, however, signs have emerged that these 2 subfields may benefit from closer conversation, as emerging approaches in both statistical genetics and phylogenetics encounter questions that call for the other subfield’s expertise. For example, in humans, evolutionarily conserved sequences are enriched for trait and disease heritability [ 48 , 49 ], and conservation across related species can be used to prioritize medically relevant variants in fine mapping [ 50 , 51 ] and rare-variant association studies [ 52 , 53 ]. Similarly, multispecies alignments are now used by conservation geneticists to estimate the fitness effects of mutations in wild populations [ 54 , 55 ] and by plant breeders to aid in genomic selection [ 56 , 57 ]. And there is growing interest in using estimated ancestral recombination graphs (ARGs) to perform explicitly tree-based versions of QTL mapping and complex trait analysis [ 58 , 59 ]. From the phylogenetics side, researchers are increasingly employing GWAS-like approaches (“PhyloG2P” methods; [ 60 ]) for mapping phenotypes of interest for which the variation primarily segregates among rather than within species.

Such emerging connections suggest that it would be beneficial to understand the ways in which statistical genetics and phylogenetic comparative biology relate to each other. Here, we show that methods in these 2 fields can be understood as closely related special cases of the same more general model. In Section 2.1, we start from first principles and develop a general statistical model for investigating associations between focal variables while controlling for shared ancestry. Then, in Section 2.2, we outline how this general model specializes to the settings of GWAS by assuming genotypes and effect sizes are conditionally independent (Section 2.2.1); animal breeding by assuming known pedigree relationships (Section 2.2.2); expected relatedness given a fixed coalescent tree (Section 2.2.3); and phylogenetics given a fixed species tree (Section 2.2.4). Next, in Section 2.3, we provide both theoretical (Section 2.3.1) and simulation-based (Section 2.3.2) demonstrations of when and how different commonly used approaches to controlling the effects of population structure succeed and fail on different timescales. Finally, in Section 2.4 we show an application of a commonly used tool of statistical genetics in a phylogenetic setting to demonstrate the utility of understanding the connections between these methodological traditions.

2.1. A standard model for a quantitative trait

For the rest of the paper, our focus will be on the first term, Cov( A i , A j ), the covariance in phenotypes between individuals due to genetic covariance. We focus on this term because, as we show subsequently, many models used by both statistical geneticists and phylogenetic biologists can be understood without reference to the components that include environmental effects. There are some circumstances in which genetic covariance in Eq 6 is undefined, such as when effect sizes have an undefined variance [ 61 ], or under certain phenomenological models of evolution on phylogenies [ 62 , 63 ]; we reserve these situations for future work and focus on situations in which the genetic covariance is finite in the subsequent sections.

2.2. Conceptualizations of the genetic covariance among individuals

The first term arises from the correlations between individuals at single loci, whereas the second term arises from correlations among loci between individuals. We focus on the first term, and all derivations below assume the second term is equal to zero, despite the fact that it will generally not be identically zero in realistic situations. As with gene-environment correlation in the previous section, many conceptualizations of genetic covariance used in practice can be viewed as neglecting the second term. Under a neutral model, the second term is 0 in expectation over distinct realizations of the evolutionary process, and its variance does not grow with the number of loci under commonly studied forms of population structure [ 64 , 65 ]. Intuitively, this term disappears in expectation under neutral evolution because the effect sizes and genotypes are uncorrelated, and hence the sum is of a mix of positive and negative terms, which cancel out on average, although it will likely be non-zero in any particular data set. Nonetheless, the second term in Eq 4 will often be nonzero in practice, and systematic correlations among loci that make the term nonzero in expectation can arise in biologically realistic situations, for example, if directional selection acts on polygenic traits. If a population experiences directional selection on a highly polygenic phenotype, much of the phenotypic change, compared with a related population that has not experienced such selection, is due to to small, coordinated changes in allele frequency, leading to systematic covariances among loci, even if they are unlinked [ 65 , 66 ]. Although we do not discuss these complications here, linkage can affect the evolution of polygenic traits [ 67 ] and the results of heritability estimates [ 68 ].

Nonetheless, by making assumptions about the evolutionary process, we can obtain useful approximations of the genetic covariance. As an example, developed further below, consider a model in which mutation and selection act on a quantitative trait. The effect size of a locus, β l , might be modeled as being drawn from a distribution, and its allele frequency p l then could evolve according to a model that depends on β l . Then, genotypes G il and G jl are drawn according to allele frequency and possibly other features. In this scenario generally, the relationship between β l and G il may be complicated. However, if selection is sufficiently weak as not to disrupt Hardy–Weinberg proportions or linkage equilibrium, then genotype frequencies depend only on the allele frequency, p l . In that case, we might represent the situation with a simplified causal graph β l → p l → G il , in which β l and G il are conditionally independent given the allele frequency p l [ 71 – 73 ].

This formula applies as long as the genetic covariance exists and the evolutionary model admits a variable Z that accounts for the relationship between effect sizes and genotypes (and all the relevant expectations exist). Moreover, it applies when the variable Z = β or Z = G .

Below, we will explore how applications across statistical and evolutionary genetics specialize Eq 5 in different ways to create a matrix summarizing genetic covariance relevant to phenotypic variation, which we refer to as Σ. In a sample of n individuals (or n species), Σ is n × n , and Σ ij is proportional to some version of Eq 5 . We will see that assumptions made in different fields relate to the underlying evolutionary process shaping genetic and phenotypic variation. Among other names, in different settings, Σ might take the form of a “genetic relatedness matrix,” “kinship matrix,” “expected genetic relatedness matrix,” or “phylogenetic variance-covariance matrix.” Below, we consider the off-diagonal entries of each of these matrices in turn.

2.2.1. The genetic relatedness matrix.

2.2.2. The (pedigree-based) kinship matrix.

Methods based on this formulation include the “animal model” [ 81 , 83 , 85 , 86 ], a widely used approach for prediction of breeding values in quantitative genetics. The connection between the animal model and genome-wide marker-based approaches was plain to the quantitative geneticists who first developed marker-based approaches to prediction [ 78 ], and it is also noted in papers aimed at human geneticists [ 22 , 74 , 87 ], whose initial interest in the framework focused on heritability estimation. Similarly, the animal model is known to be intimately connected to the phylogenetic methods we discuss later [ 40 – 42 ]. One implication is that close connections between methods used in statistical genetics and phylogenetics, which are our focus here, must exist.

2.2.3. The expected genetic relatedness matrix (eGRM).

In principle, the entries of the relatedness matrix could be computed on the basis of a demographic model; in this approach, one would average over both random gene trees and random mutations. This is the approach used by McVean [ 89 ] to provide a genealogical interpretation of principal components analysis in genetics.

In a related approach, several recent methods in statistical genetics [ 58 , 59 , 90 ] and in phylogenetics [ 91 ] take as input a genome-wide inference of local gene trees. If the gene trees are treated as known, then the only source of randomness is the placement of mutations, as in equation S7, and averaging over trees is accomplished by taking an average over the estimated gene trees. For example, Link and colleagues [ 58 ] compute the expectation of a local GRM (i.e., a local eGRM) conditional on estimated gene trees in a region of the genome. These local eGRMs are then used as input to a variance-components model, which brings some advantages in mapping QTLs. Specifically, the resulting (conditional) expected genetic relatedness matrices naturally incorporate LD, providing better estimates of local genetic relatedness than could be formed from a handful of SNPs in a local region [ 58 , 90 ].

2.2.4. The phylogenetic variance-covariance matrix.

Consistent with previous arguments (e.g., [ 35 ]), this result also implies that one interpretation of the standard PGLS model is that it stratifies the regression between focal variables by an unobserved variable (or variables) that evolved primarily by drift. Hansen and colleagues have pointed out that this may not be an appropriate model for testing for adaptation [ 32 , 33 , 96 ], which was the primary motivation for developing many comparative methods in the first place [ 97 ]. Moreover, recently, standard PGLS has come into question in scenarios in which there is discordance between the gene tree and the species tree [ 98 – 100 ]. Our formulation makes it clear that the standard PGLS formulation only applies when there is a single tree underlying all loci; if there is instead a distribution of gene trees, equation S8 suggests that the appropriate thing to do is to average over gene trees, as suggested by Hibbins and colleagues [ 99 ], and as done in a statistical genetics setting [ 58 , 59 ]. However, one difficulty is deciding over which gene trees one should average, particularly if the trait is oligogenic [ 100 ].

2.2.5. Connections among different approaches to modeling genetic contributions to phenotypic covariance.

Fig 1 provides a conceptual picture of how the various approaches are related to each other. The left side shows the situation typical in genome-wide association settings: SNP genotypes, shown as a matrix of variable sites with derived alleles colored in red, are determined by the topologies of gene trees and the mutations that fall on them. The GRM is computed on the basis of the SNP genotypes, as in Eq 12 . If gene trees are known, then the eGRM can be computed by averaging over Poisson placement of mutations as in equation S7 over gene trees. If only a demography is known, both gene trees and mutations can be averaged over using coalescent theory, as in equation S8. The right-hand side shows the situation in phylogenetics: on a single fixed tree, the population trait mean evolves according to a Brownian motion. This results in a multivariate Gaussian distribution of phenotypes across species. We show that the covariance predicted by the Brownian motion model is equivalent to the covariance predicted by averaging over Poisson distributed mutations on a gene tree that is fixed to coincide with the species tree. In the figure, we highlight bifurcating population trees for simplicity and clarity, but the results also apply in complex demographic scenarios with admixture and reticulation.

• PPT PowerPoint slide
• PNG larger image
• TIFF original image

The left-hand side shows the situation when multiple samples are taken from each group, as is the case in a genome-wide association study. The population tree is indicated by bold lines, and inside of it gene trees are indicated by thinner lines. Mutations on the gene trees are indicated by purple lightning bolts. The mutations on the gene tree result in genotype matrices, shown as one 2 × 5 array per species, with purple-filled entries indicating mutations. The right-hand side shows the situation in phylogenetics, where the species mean phenotype, indicated by a thin squiggly line, evolves according to a Brownian motion within a species tree, indicated by bold lines. The distribution of possible phenotypes within each species is marginally Gaussian.

https://doi.org/10.1371/journal.pbio.3002847.g001

2.3. How the same type of unmodeled structure misleads both GWAS and phylogenetic regressions

That standard models in statistical genetics and phylogenetics are deeply related immediately suggests that these models might suffer the same pathologies under model misspecification, and that solutions to these pathologies could be shared across domains. Here, we illustrate this by studying the problem of how unmodeled (phylo)genetic structure biases estimates of regression covariates. This problem has received much attention in both the statistical genetics [ 101 , 102 ] and phylogenetics literature [ 34 , 35 , 103 ], but the approaches taken in the 2 fields differ.

2.3.1. Theoretical analysis.

This shows that we can conceptualize the ordinary least squares estimator as adding up the correlations between x and y projected onto each eigenvector of Σ. Loosely, large-magnitude slope estimates arise when x and y both project with large magnitude onto one or more eigenvectors of Σ. If an eigenvector of Σ is correlated with a confounding variable, such as the underlying (phylo)genetic structure, then x and y may both have substantial projections onto it, even if x and y are only spuriously associated due to the confound.

Two seemingly distinct approaches have been proposed to address this issue. First, researchers have proposed including the eigenvectors of Σ as covariates. In the phylogenetic setting, this is known as phylogenetic eigenvector regression [ 104 ]. (In practice, researchers often use the eigenvectors of a distance matrix derived from the phylogenetic tree rather than Σ itself, but these 2 matrices have a straightforward mathematical connection [ 105 ].) In the statistical genetics setting, the analogous approach is to include the principal component projections of the data that are used to generate the genetic relatedness matrix—i.e., the principal components of the genotype matrix [ 23 ]—in the regression. For completeness, in Section D in S1 Text we show that these 2 approaches include the same covariates, up to a scaling factor.

This is straightforwardly the OLS estimator ( Eq 15 ), except that the first J eigenvectors of Σ are removed. This shows why inclusion of the eigenvectors of Σ as covariates can correct for (phylo)genetic structure: it simply eliminates some of the dimensions on which x and y may covary spuriously. However, it also shows the limitations of including eigenvectors as covariates. First, because it is simply cutting out entire dimensions, it can result in a loss of power. Second, confounding that aligns with eigenvectors that are not included in the design matrix is not corrected.

Like the ordinary least squares estimator in Eq 18 , this expression includes all the eigenvectors of Σ. However, it downweights each eigenvector according to its eigenvalue. Thus, GLS downweights dimensions according to their importance in Σ, which aims to describe the structure according to which x and y may be spuriously correlated. However, unlike Eq 16 , it retains all dimensions. Compared with adjusting for the leading eigenvectors of Σ using OLS, the GLS approach retains some ability to detect contributions to associations that align with the leading eigenvectors. It also adjusts for Σ in its entirety, rather than just its leading eigenvectors. This means that it adjusts for even very recent (phylo)genetic structure, which will likely not be encoded by the leading eigenvectors. That said, one disadvantage of GLS is that it assumes that all eigenvectors of Σ contribute to confounding in proportion to their eigenvalues, potentially resulting in an inability to completely control for confounding if the effect of an eigenvector of Σ is not proportional to its eigenvalue, as may be the case with, for example, environmental confounding. In other words, the cost of including some adjustment for every eigenvector of Σ is an assumption as to how these eigenvectors relate to confounding.

Thus, using the eigenvectors of Σ as covariates in a generalized least squares framework may provide the benefits of both approaches: if there is confounding in a eigenvector of Σ that is “too large”—that is, it is out of proportion with its associated eigenvalue—then if that eigenvector is included in the design matrix, it will simply be excised from the estimator, as in Eq 17 . However, we still maintain the ability to control for spurious association between x and y due to the structure of Σ but not along included eigenvectors, as in Eq 17 . The major difficulty is in identifying the eigenvectors of Σ that might be associated with confounding effects larger than their corresponding eigenvalues would suggest.

2.3.2. Simulation analysis.

To put the intution developed from the previous subsection into practice, we performed simulations in both phylogenetic and statistical-genetic settings. First, to explore how the approaches outlined above correct for both (phylo)genetic structure and environmental confounding, we performed simulations inspired by Felsenstein’s “worst case” scenario [ 35 , 46 ]. Felsenstein’s worst case supposes that there are 2 diverged groups of samples that are measured for 2 variables x and y , which are then tested for association; the only (phylo)genetic structure is between the 2 groups. In the phylogenetic setting, we represent the 2 clades as star trees with 100 tips each, connected by internal branches, and we simulate x and y as arising from independent instances of Brownian motion along the tree (see Methods ). In the statistical genetics setting, we use msprime [ 115 ] to simulate 100 diploid samples from each of 2 populations, and then simulated quantitative traits using the alpha model [ 22 ] (see Methods ). In this setting, McVean [ 89 ] showed that the first eigenvector of Σ captures population membership; hence, we only include the first eigenvector to capture any residual confounding. To perform inference in the phylogenetic case, we used the package phylolm [ 110 ], and for the statistical-genetic case, we used a custom implementation of REML [ 74 ].

We first explored the impact of deepening the divergence between the 2 clades, starting from no divergence and increasing to high divergence ( Fig 2A and 2C ). As expected, we see ordinary least squares fails to control for the population stratification as the divergence time becomes large, resulting in excessive false positives. However, all of the other approaches appropriately controlled for the population stratification. This is as expected: in the case of 2 populations, all of the (phylo)genetic stratification is due to the accumulation of genetic variants in each group. Hence, either discarding the correlation between x and y on the dimension corresponding to group membership as in Eq 16 or downweighting it as in Eq 18 is sufficient to remove the confounding effect of the population stratification.

(A) A depiction of Felsenstein’s worst case in the phylogenetic setting. A Brownian motion evolves within a species tree separating 2 clades. For simplicity, 2 tips are shown in each clade; in the simulations, each clade contains 100 tips. The purple arrow shows a simulated singular evolutionary event (see text). (B) The false positive rate of each method in a simulated phylogenetic regression as a function of divergence time between the 2 groups. The horizontal axis shows the divergence time, while the vertical axis shows the fraction of tests that would be significant at the 0.05 level. Each line represents a different method. The lines for OLS + Eig1 and PGLS + Eig1 are completely overlapping. (C) The false positive rate of each method in a simulated phylogenetic regression as a function of the size of non-Brownian shifts in both predictor and response variables. The horizontal axis shows the standard deviation of the normal distribution from which the shift was drawn, and the vertical axis shows the fraction of tests that would be significant at the 0.05 level. The lines for OLS + Eig1 and PGLS + Eig1 are completely overlapping. (D) A depiction of Felsenstein’s worst case in the statistical genetic setting. Gene trees with mutations are embedded within a population tree depicting 2 divergent populations. For simplicity, 2 samples are shown within each population; in the simulations, each population consists of 100 diploid individuals. The purple arrow shows a simulated environmental effect (see text). (E) The false positive rate of each method in a simulated GWAS as a function of divergence time between the 2 groups. The horizontal axis shows the divergence time, while the vertical axis shows the fraction of tests that would be significant at the 0.05 level. Each line represents a different method. (F) The false positive rate of each method in a simulated GWAS as a function of the size of an environmental shift. The horizontal axis shows the standard deviation of the normal distribution from which the shift was drawn, and the vertical axis shows the fraction of tests that would be significant at the 0.05 level. Underlying data can be found at https://zenodo.org/records/13774370 .

https://doi.org/10.1371/journal.pbio.3002847.g002

Despite the success of both OLS with eigenvector covariates and generalized least squares in controlling for population stratification, it has recently been recognized that phylogenetic generalized least squares does not control for all types of confounding in Felsenstein’s worst case: for example, if there is a large shift in x and y on the branch leading to one of the groups, phylogenetic generalized least squares produces high false positive rates [ 35 ]. Because including the first eigenvector of Σ will completely eliminate the contribution to the estimated coefficient that projects on group membership, whereas generalized least squares will only downweight it, we reasoned that including the first eigenvector in either ordinary or generalized least squares should restore control even in the presence of large shifts.

We tested our hypothesis using simulations with divergence time in which ordinary least squares was not sufficient to correct for population stratification. In the phylogenetic case, we simulated an additional shift in one of the clades for both x and y by sampling from independent normal distributions, while in the statistical-genetic case, we simulated an environmental shift sampled from a normal distribution in one of the clades ( Fig 2B and 2D ). As expected, ordinary least squares is insufficient to address the confounding, and becomes increasingly prone to false positives as the size of the shift increases. In line with our hypothesis, phylogenetic generalized least squares and linear mixed modeling also fail to control for the shift as it becomes large, while including just a single eigenvector in each case is sufficient to regain control over false positives.

The preceding analysis might suggest that including eigenvectors of Σ as covariates is sufficient to adjust for (phylo)genetic structure while also being superior to generalized least squares in dealing with environmental confounding. Recent work, however, suggests that inclusion of principal components may not be able to adjust for more subtle signatures of population structure [ 8 , 15 , 102 , 116 ]. To explore this, we simulated both phylogenetic regression and a variant association test using a more complicated model of population structure. For the phylogenetic case, we simulated pure birth trees with 200 tips, while in the statistical genetics case, we simulated pure birth trees with 20 tips and sampled 10 diploids from each tip using msprime . Then, as before, we simulated using a Brownian motion model in the phylogenetic case, or an additive model for the statistical genetic case.

As expected, using ordinary least squares without any eigenvector covariates does not control for population structure in either the phylogenetic or the statistical-genetic setting, but the methods that use generalized least squares estimates of the regression coefficients appropriately model population structure ( Fig 3 ). Although adding additional eigenvectors reduces the false positive rate of ordinary least squares, false positives are not reduced to the nominal level of 5%. This is in line with our theoretical analysis: as seen in Eq 16 , including eigenvectors in ordinary least squares eliminates dimensions that explain the most genetic differentiation, but the correlations on the remaining dimensions are not adjusted. Because there is substantial fine-scale population structure in these simulations, removal of just a few dimensions with large eigenvalues is not sufficient to control for the subtle signature of population structure. In the phylogenetic setting, we expect that including additional eigenvectors would eventually gain control of false positives, but it may require including all of the eigenvectors and result in an overdetermined problem. On the other hand, in the population-genetic simulations, including additional eigenvectors will not increase control over false discoveries. There are 2 reasons for this. First, because Σ is estimated from the genetic data, the eigenvectors themselves are estimated. In practice, this means that eigenvectors corresponding to small eigenvalues are estimated poorly. Second, because we have 200 samples but only 20 populations, many of the samples share the same evolutionary history, and hence several eigenvectors share the same eigenvalue “in theory”—that is, if viewed from the perspective of the population tree rather than the realized gene trees or genotypes. Roughly speaking, in this simulation, there are only approximately 20 eigenvectors that correspond to “true” confounding. In practice, due to randomness of mutations and gene trees, the remaining eigenvectors will not share identical eigenvalues, but will nonetheless correspond to genetic differentiation of individuals with shared evolutionary history, and hence will not correct for genetic confounding. This is reminiscent of the observations that in some human genetics data sets, only the first few eigenvectors stably capture genetic differentiation [ 5 ], and that LMM approaches become increasingly necessary when the sample includes relatively close genealogical relatives, whose relatedness is captured in the GRM but will not typically affect its leading eigenvectors [ 102 ].

(A) Performance of ordinary least squares and phylogenetic least squares in a model with 200 tips related by a pure birth tree. The horizontal axis shows the number of eigenvectors included as covariates, and the vertical axis shows the fraction of tests that would be significant at the 0.05 level. (B) Performance of ordinary least squares and a linear mixed model in a model with 20 populations related by a pure birth tree and 10 diploid individuals per population. The horizontal axis shows the number of eigenvectors included as covariates, and the vertical axis shows the fraction of tests that would be significant at the 0.05 level. Underlying data can be found at https://zenodo.org/records/13774370 .

https://doi.org/10.1371/journal.pbio.3002847.g003

In contrast to including eigenvectors as fixed effects as part of an OLS analysis, generalized least squares approaches, as shown in Eq 18 , will continue to correct for population structure that is found deeper into the eigenvectors of the correlation matrix (echoing points previously raised in the phylogenetics literature [ 117 – 119 ]). We also note that while the our analysis is focused on the eigenvectors of Σ, we suspect similar lines of reasoning may apply to other situations in which eigenvector regression is used, such as in spatial ecology [ 120 ].

2.4. A case study of including eigenvectors as covariates in PGLS

Although the eigenvectors of the phylogenetic variance-covariance matrix (or closely related quantities) have often been included in regression models by researchers using phylogenetic eigenvector regression [ 104 ], to the best of our knowledge, phylogenetic biologists have not previously used these eigenvectors as fixed effects in a PGLS model, which we have shown above to be a potentially effective strategy in theory. To illustrate the approach in practice, we re-examine a recent study by Cope and colleagues [ 121 ] that tested for coevolution in mRNA expression counts across 18 fungal species. More specifically, these researchers were interested in testing whether genes whose protein products physically interacted (using independent data from [ 122 ]) were more likely to have correlated expression counts than those whose protein products did not. They found support for this prediction. While we suspect the core finding is robust, and there are some theoretical reasons to expect that RNA expression counts should be Brownian-like under some selective scenarios [ 123 ], other studies have shown expression counts for many genes in this data set (and many others) are not well described by a Brownian process [ 124 , 125 ]. As such, some of their observed correlations could be spurious due to unmodeled phylogenetic structure [ 35 ].

We re-analyzed the data of Cope and colleagues [ 121 ] with the addition of the eigenvectors of (phylogenetic) Σ as fixed effects in the PGLS model (see Methods and materials for details). Cope and colleagues used a correlated multivariate Brownian model to test their hypothesis, which is slightly different from the more common PGLS approach [ 126 ], but they are close enough for our purposes. We conducted several iterations of the analyses, varying the number of eigenvectors included from 1 to 10; Fig 4A shows how the different species project onto each principal component. We found that, as anticipated, the number of significant correlations decreased as more eigenvectors were included ( Fig 4B ). However, as more eigenvectors were included, the proportion of significant correlations in gene-expression count data in which the genes are known to physically interact increased (up to about 8 eigenvectors; Fig 4C ). If we assume that the significant correlations for physically interacting genes are more likely to be true positives than those for pairs of genes not known to interact physically, then the results would suggest that including the eigenvectors in the analysis might reduce the false positive rate while still finding many of the true positives.

(A) The fungal tree; colors indicate each species’ position in the first 10 dimensions of principal component space. (B) The overall number of significant pairs decreases as more eigenvectors are included in the regression. The horizontal axis indicates the number of eigenvectors included as fixed effects, and the vertical axis shows the proportion of significant pairs compared with a model that includes no eigenvectors as fixed effects. (C) The enrichment of known binding pairs as a function of eigenvectors included. The horizontal axis indicates the number of eigenvectors included as fixed effects, and the vertical axis shows the enrichment of known binding pairs relative to a model in which no eigenvectors are included. Underlying data can be found at https://zenodo.org/records/13774370 .

https://doi.org/10.1371/journal.pbio.3002847.g004

Uyeda and colleagues [ 35 ] suggest that one way to mitigate the spurious correlations arising from large, unreplicated events would be to include indicator variables in the regression model that encode the part of the phylogeny from which a tip descends. This is similar in spirit to the use of hidden Markov models for the evolution of discrete traits [ 103 , 127 ]. However, as Uyeda and colleagues point out, this leaves open the hard problem of identifying the branches on which to stratify. It is not possible to include an indicator for every branch, as the model would then be overdetermined. Using the simple method borrowed from GWAS studies of including eigenvectors of Σ as fixed effects in the typical phylogenetic regression may be a promising (partial) solution to the problem of spurious correlations.

3. Discussion

3.1. the genetic model versus the statistical model.

We began by adding assumptions to a general model of a polygenic trait ( Eq 2 ) in order to show that common practices in disparate areas of genetics can be seen as special cases of the same model. One notable assumption is that of a purely additive model [ 128 ] for the phenotype ( Eq 1 ). There are 2 reasons we might be suspicious of this assumption. First, it is debatable to what extent most traits obey the additive model, given evidence of non-additive genetic contributions to traits across species [ 129 , 130 ]. However, even if non-additive contributions are important for determining individual phenotypes or for understanding traits’ biology, they might still contribute a relatively small fraction of trait variance, meaning they might be safely ignored for some purposes [ 131 – 133 ] (but see [ 134 ]). Second, we used a neutral coalescent model to find an expression for the Brownian motion diffusion parameter in terms of the effect sizes of individual loci ( Eq 13 ). Although this provides a satisfying justification for the use of a phylogenetic regression model with a Brownian covariance structure and for averaging over gene trees to accommodate ILS ( sensu [ 99 ]), it is likely unreasonable in many situations. It has long been appreciated that, while a population-mean phenotype will be expected to evolve according to a Brownian process under simple quantitative-genetic models of genetic drift [ 43 , 92 , 95 , 135 ] the Brownian rate estimated from phylogenetic comparative data is orders of magnitude too slow to be consistent with plausible values for the quantitative-genetic parameters used to derive the Brownian model [ 95 , 135 – 137 ]. There are more elaborate explanations than pure genetic drift for why long-term evolution may show relatively simple dynamics [ 138 ] but understanding the coalescent patterns of loci under these scenarios is likely challenging [ 139 ] and beyond the scope of the present paper.

However, even if one finds the genetic model unreasonable, the equivalence of the statistical models used in statistical genetics and phylogenetics still holds: that is, the core structures of the models are the same, whether one is willing to interpret the parameters in the same way or not. Indeed, phylogenetic biologists have been here before, with the realization that PGLMMs are structurally equivalent to the pedigree-based analyses using the animal model from quantitative genetics [ 40 – 42 ] even though the recognition that they were equivalent did not rely on a specific genetic model for phenotypes. (We showed here that they can both be derived from the same genetic model.) Nonetheless, the recognition of a structural equivalence between the animal model and the phylogenetic model made it possible to use techniques from quantitative genetics to solve problems in phylogenetic comparative methods. For example, inspired by a similar model from [ 140 ], Felsenstein developed a phylogenetic threshold model [ 141 , 142 ], in which discrete phenotypes are determined by a continuous liability that itself evolves according to a Brownian process. Hadfield [ 143 ] proved this model was identical to a variant of the animal model and that existing MCMC algorithms could be used to efficiently estimate parameters and extend the threshold to the multivariate case, which had not been previously derived.

3.2. Towards a more integrative study of the genetic bases of phenotypes

Building a general framework is a step towards inference methods that coherently integrate intra- and interspecific variation to understand the genotype-to-phenotype map and how evolutionary processes, acting at different time scales, shape it. Indeed, the importance of evolutionary conservation in triaging functional variants in the human genome has long been appreciated and is becoming increasingly important as we collect larger samples of people; the same is true for the use of genomics in agriculture [ 57 ] and conservation genetics [ 55 ]. Recent work showed that evolutionary conservation accounts for the vast majority of the predictive power of a state-of-the-art deep learning approach to variant annotation [ 144 , 145 ]. But most of the cutting-edge phylogenomic approaches for triaging variants typically do not use the phylogeny at all (i.e., only multiple sequence alignments [MSAs] are used), or include the phylogeny without an explicit evolutionary model [ 146 ]. This is a limitation because we are not making the most of the information in the tree, nor are we able to draw specific inferences about how evolutionary processes have shaped complex traits from the MSA alone. Overcoming this limitation is not straightforward and will require mechanistic modeling: The observed level of conservation is a nonlinear function of the strength of selection acting against variants at a locus; small changes in the strength of negative selection can greatly decrease the amount of variability seen on phylogenetic timescales, and this can cause counterintuitive behavior of conservation scores [ 54 , 147 ].

A key difficulty in combining information across timescales arises from different assumptions about the evolutionary process. For example, the canonical GRM in statistical genetics assumes that the variance of an allele’s effect size is inversely proportional to the heterozygosity at the locus. As we show in Section A in S1 Text , this assumption can be justified under a model of mutation-selection balance with Gaussian stabilizing selection on a single trait. However, we do not generally understand how robust such approaches are under more complex (and realistic) evolutionary scenarios that include the influence of genetic drift and selection on genetically correlated traits, nor how errors influence downstream inferences [ 71 , 76 , 148 , 149 ]. There is substantial evidence that rarer variants tend to have larger effect sizes [ 76 , 150 – 155 ], which is broadly consistent with the motivation for the canonical GRM and for the more general α model, which supposes that the variance of the effect size of an allele is given as a power law function of its heterozygosity [ 22 , 68 , 74 , 76 ]. (Although we show here that setting α = 1 can be motivated by a model of stabilizing selection on a single trait and ignoring genetic drift, the more general α model is not derived from an evolutionary model.) However, close examination of GWAS effect sizes suggests a poor fit of the α model for many traits [ 148 ], and it has been suggested that more complex models might better capture the wide variation of effect sizes [ 155 ]. Further, recent explosive human population growth has resulted in a massive number of rare variants [ 156 – 160 ]—assuming that there is substantial input of selectively neutral mutations, some of these rare variants will be rare not because they have been driven to or held at low frequency by selection, but simply because they represent the effect of population growth on the neutral site-frequency spectrum. As such, using the alpha model may result in overestimation of heritability for traits where there is a substantial contribution of genetic drift and may result in incompletely controlled confounding in trait mapping studies. And although effect sizes of individual causal variants can be estimated well for common variants, this is unlikely ever to be possible for sufficiently rare variants; hence, a realistic model of effect sizes as a function of allele frequency is necessary for inclusion in efforts such as rare-variant association studies [ 52 , 161 – 163 ].

In contrast, in our derivation of gene-tree (i.e., those using the eGRM) and phylogenetic (i.e., using the phylogenetic variance-covariance matrix) model, we assumed that effect sizes and genotypes were independent, and that trait-affecting mutations fall on gene trees as a Poisson process [ 89 ]. These assumptions are justified if the causal variants are neutral. But the neutrality assumption contradicts a wealth of evidence from both within and among species that quantitative trait variation is under some form of selection [ 164 – 171 ] and that the effect sizes of causal variants tend to be larger in more evolutionarily conserved regions [ 50 , 144 , 172 – 175 ], which also implies an important role of purifying selection. The α model, or presumably other models of the relationship between effect size and allele frequency, can be incorporated in an eGRM [ 59 , 90 ]. After all, an eGRM is an expectation (under Poisson-process mutation) of a GRM, and so any scaling applied to genotypes in computing the GRM can be made to apply to the eGRM. But the interpretation becomes complicated, since the assumption that mutations accrue on the tree as a Poisson process is still being relied upon.

One way phylogenetic biologists include selection is by modeling the evolution of quantitative traits with an Ornstein–Uhlenbeck (OU) process [ 96 , 176 – 179 ], which can be derived from a quantitative-genetic model of stabilizing selection [ 92 ], although in practice, the OU model is often interpreted as a phenomenological model of the evolution of the adaptive peaks [ 44 , 180 ]. Many researchers have used the Σ matrix derived from an OU process in PGLS models [ 176 , 181 ]; this is straightforward because the data remain multivariate Gaussian [ 39 , 110 ]. One could potentially use an analogous approach to model phenotypic evolution along gene trees within a species (to inform the construction of eGRM, for example). Such an approach could improve inferences from both tree-based GWAS (sensu [ 58 , 59 ]) and from emerging phylogenetic comparative approaches that consider gene trees rather than just the species trees [ 98 , 99 , 182 ] (such approaches are important as only using a single species tree may lead one to mistake similarity due to common ancestry for convergence [ 100 , 183 – 185 ]). However, identifying the correct form of the model would likely require an analysis of the ancestral selection graph [ 139 , 186 ], a notoriously challenging theoretical endeavor.

In sum, an implication of our results is that standard approaches in both statistical genetics and phylogenetic comparative methods incorporate assumptions that are plausibly motivated under neutrality but questionable under various forms of selection—ignoring covariances among loci (the second term in Eq 4 ), placing mutations on the tree as a Poisson process, invoking Brownian motion, etc. Common practices in both fields—e.g., normalizing genotypes by their heterozygosity or using OU processes—can be motivated by simple models that include selection, but they do not constitute a principled approach to incorporating drift and selection into models of trait covariance. In particular, the considerations that lead to them are not sufficiently general (e.g., normalizing by heterozygosity does not incorporate drift or pleiotropy), and they are sometimes used in combination with maneuvers that arise from incompatible assumptions. Developing more robust evolutionary-genetic models of genetic contributions to trait covariance is a formidable challenge, but it may lead to stronger statistical practices that can be used in both micro- and macroevolutionary studies.

We suspect that there are additional connections between statistical genetics and phylogenetics that we have not mapped out here and that could be profitably explored. For example, in most of the applications in which phylogenomic data are used to inform mapping studies, researchers have large-scale phenotypic and genomic sampling for a focal population or species and then sparser genomic sampling (often a single genome) and an estimate of phenotypic means (if even that) for the others. However, there are emerging data sets from closely related species that have dense phenotypic and genomic samples from multiple lineages [ 187 , 188 ]. We anticipate that our framework could be used to derive more principled and powerful approaches for analyzing these types of data. At the other extreme are methods in which we have sparse sampling of both phenotypes and genomes for a phylogenetically diverse set of species (which generally fall under the PhyloG2P label, mentioned above [ 60 ]). In this case, researchers either use phylogenetic data to uncover convergent mutations associated with phenotypic convergence across lineages (e.g., [ 189 ]) or more commonly, identify regions with a relatively large number of substitutions—but not necessarily the same ones—in phylogenetically distinct lineages that have convergently evolved the same phenotype [ 190 , 191 ]. For example, Sackton and colleagues [ 192 ] used such an approach to identify regulatory regions that had high rates of evolution in lineages of flightless birds; they also demonstrated that some of these regions influence wing development using experimental perturbations. Such rate association tests (see also [ 193 ]) seem to be very similar, both conceptually and statistically, to techniques used in rare-variant association studies, which look for local enrichment of rare variants in cases versus controls, rather than associating single variants with phenotype [ 52 , 161 – 163 ]. We suspect that one could derive a formal equivalence between these sets of methods as we did between GWAS and PGLS above using similar techniques.

There are clear biological rationales explaining why various types of analyses will be more or less informative at different timescales. But this is a difference of degree and not of kind. And the different methodological traditions in statistical genetics and phylogenetics are just that—traditions. There is no reason that researchers should think about the problem of trait mapping in fundamentally distinct ways just because they happened to be trained in a statistical genetics or phylogenetics lab. Ultimately, we should work to take the best ideas from both of these domains and blend them into a more cohesive paradigm that will clarify the molecular bases of phenotypes.

4. Materials and methods

4.1. simulation details.

To perform phylogenetic simulations, we used the fastBM function from the phytools R package [ 194 ]. In all cases, Brownian motions were simulated independently and with rate 1. When performing phylogenetic simulations of Felsenstein’s worst case, we used stree from ape [ 195 ] to simulate 2 star trees of 100 tips, where each tip in the star tree had length 0.5. We then connected the 2 star trees using internal branches of varying length. To add a non-Brownian confounder, in each simulation we added an independent normal random variable with varying standard deviations to the x and y values for individuals from clade 1. (Within a given simulation, all individuals in clade 1 were augmented by the same value for each trait, while between simulations, the confounding effect was a random draw.) When performing simulations in a more complicated phylogeny, we used TreeSim [ 196 ] to generate pure-birth trees with birth rate = 1 and complete taxon sampling. Each simulation replicate used a different tree. For ordinary least squares on phylogenetic data, we used the R function lm . For PGLS on phylogenetic data, we used the R package phylolm [ 110 ] with the Brownian motion model and no environmental noise.

4.2. Phylogenetic analysis of yeast gene expression data

We obtained the species tree, gene expression matrix, and list of physically interacting genes from https://github.com/acope3/GeneExpression_coevolution [ 121 ]. We then randomly subsampled 500 genes that had measurements in at least 15 of the 20 species to test for association, resulting in 124,750 pairs. Because of differential missingness among genes, we computed phylogenetic eigenvector loadings only on the subtree for which both genes had data present, meaning that each pair may have had slightly different eigenvector loadings. We then used phylolm [ 110 ] with no measurement error to estimate the regression coefficient. For each number of eigenvectors included, we corrected for multiple testing by controlling the FDR at 0.05 using the Benjamini–Hochberg procedure [ 197 ].

Supporting information

S1 text. complete derivations of results..

https://doi.org/10.1371/journal.pbio.3002847.s001

Acknowledgments

We thank Alvina Adimoelja, Matt Aguirre, Garyk Brixi, Graham Coop, Emily Josephs, Nikhil Milind, Roshni Patel, Molly Przeworski, Katalin Voss, Julie Zhu, members of the Coop, Przeworski, Andolfatto, and Sella labs for helpful comments on the manuscript. We also thank Matt Hahn, Nick Mancuso, Jeff Spence, Sasha Gusev, Loren Rieseberg, and members of the Pennell, Edge, and Mooney labs for their thoughtful comments on parts of this study. Alex Cope provided additional guidance on our analysis of the yeast gene expression data.

• View Article
• PubMed/NCBI
• Google Scholar
• 6. Veller C, Coop G. Interpreting population and family-based genome-wide association studies in the presence of confounding. bioRxiv. 2023 Jan:2023.02.26.530052. Available from: http://biorxiv.org/content/early/2023/02/27/2023.02.26.530052.abstract .
• 12. Berg JJ, Harpak A, Sinnott-Armstrong N, Joergensen AM, Mostafavi H, Field Y, et al. Reduced signal for polygenic adaptation of height in UK Biobank. Elife. 2019 Mar;8:e39725. Publisher: eLife Sciences Publications, Ltd. Available from: https://doi.org/10.7554/eLife.39725 .
• 13. Sohail M, Maier RM, Ganna A, Bloemendal A, Martin AR, Turchin MC, et al. Polygenic adaptation on height is overestimated due to uncorrected stratification in genome-wide association studies. Elife. 2019 Mar;8:e39702. Publisher: eLife Sciences Publications, Ltd. Available from: https://doi.org/10.7554/eLife.39702 .
• 14. Barton N, Hermisson J, Nordborg M. Why structure matters. eLife. 2019 Mar;8:e45380. Publisher: eLife Sciences Publications, Ltd. Available from: https://doi.org/10.7554/eLife.45380 .
• 16. Blanc J, Berg JJ. Testing for differences in polygenic scores in the presence of confounding. bioRxiv. 2023 Jan:2023.03.12.532301. Available from: http://biorxiv.org/content/early/2023/08/22/2023.03.12.532301.abstract .
• 58. Link V, Schraiber JG, Fan C, Dinh B, Mancuso N, Chiang CW, et al. Tree-based QTL mapping with expected local genetic relatedness matrices. bioRxiv. 2023:2023–2004.
• 79. Mrode RA. Linear Models for the Prediction of Animal Breeding Values. 3rd ed. CABI Wallingford, Oxfordshire, UK; 2013.
• 81. Henderson CR. Applications of Linear Models in Animal Breeding. University of Guelph; 1984.
• 83. Lynch M, Walsh B, et al. Genetics and analysis of quantitative traits. vol. 1. Sinauer Sunderland, MA; 1998.
• 84. Gillespie JH. Population genetics: a concise guide. JHU press; 2004.
• 97. Harvey PH, Pagel MD, et al. The comparative method in evolutionary biology. vol. 239. Oxford University Press, Oxford; 1991.
• 100. Adams R, Lozano JR, Duncan M, Green J, Assis R, DeGiorgio M. A tale of too many trees: a conundrum for phylogenetic regression. bioRxiv. 2024. Available from: https://www.biorxiv.org/content/early/2024/02/20/2024.02.16.580530 .
• 120. Legendre P, Legendre L. Numerical ecology. Elsevier; 2012.
• 145. Benegas G, Albors C, Aw AJ, Ye C, Song YS. GPN-MSA: an alignment-based DNA language model for genome-wide variant effect prediction. bioRxiv.
• 148. Simons YB, Mostafavi H, Smith CJ, Pritchard JK, Sella G. Simple scaling laws control the genetic architectures of human complex traits. bioRxiv. 2022;p. 2022.10.04.509926.
• 155. Spence JP, Sinnott-Armstrong N, Assimes TL, Pritchard JK. A flexible modeling and inference framework for estimating variant effect sizes from GWAS summary statistics. bioRxiv. 2022. Available from: https://www.biorxiv.org/content/early/2022/04/19/2022.04.18.488696 .
• 180. Hansen TF. Adaptive landscapes and macroevolutionary dynamics. In: Svensson E, Calsbeek R, editors. The adaptive landscape in evolutionary biology. Oxford University Press, Oxford, UK; 2012. p. 205–226.

• Methodology article
• Open access
• Published: 20 March 2007

A practical approach to phylogenomics: the phylogeny of ray-finned fish (Actinopterygii) as a case study

• Chenhong Li 1 ,
• Guillermo Ortí 1 ,
• Gong Zhang 2 &
• Guoqing Lu 3  

BMC Evolutionary Biology volume  7 , Article number:  44 ( 2007 ) Cite this article

26k Accesses

302 Citations

3 Altmetric

Metrics details

Molecular systematics occupies one of the central stages in biology in the genomic era, ushered in by unprecedented progress in DNA technology. The inference of organismal phylogeny is now based on many independent genetic loci, a widely accepted approach to assemble the tree of life. Surprisingly, this approach is hindered by lack of appropriate nuclear gene markers for many taxonomic groups especially at high taxonomic level, partially due to the lack of tools for efficiently developing new phylogenetic makers. We report here a genome-comparison strategy to identifying nuclear gene markers for phylogenetic inference and apply it to the ray-finned fishes – the largest vertebrate clade in need of phylogenetic resolution.

A total of 154 candidate molecular markers – relatively well conserved, putatively single-copy gene fragments with long, uninterrupted exons – were obtained by comparing whole genome sequences of two model organisms, Danio rerio and Takifugu rubripes . Experimental tests of 15 of these (randomly picked) markers on 36 taxa (representing two-thirds of the ray-finned fish orders) demonstrate the feasibility of amplifying by PCR and directly sequencing most of these candidates from whole genomic DNA in a vast diversity of fish species. Preliminary phylogenetic analyses of sequence data obtained for 14 taxa and 10 markers (total of 7,872 bp for each species) are encouraging, suggesting that the markers obtained will make significant contributions to future fish phylogenetic studies.

We present a practical approach that systematically compares whole genome sequences to identify single-copy nuclear gene markers for inferring phylogeny. Our method is an improvement over traditional approaches (e.g., manually picking genes for testing) because it uses genomic information and automates the process to identify large numbers of candidate makers. This approach is shown here to be successful for fishes, but also could be applied to other groups of organisms for which two or more complete genome sequences exist, which has important implications for assembling the tree of life.

The ultimate goal of obtaining a well-supported and accurate representation of the tree of life relies on the assembly of phylogenomic data sets for large numbers of taxa [ 1 ]. Molecular phylogenies based on DNA sequences of a single locus or a few loci often suffer from low resolution and marginal statistical support due to limited character sampling. Individual gene genealogies also may differ from each other and from the organismal phylogeny (the "gene-tree vs. species-tree" issue) [ 2 , 3 ], in many cases due to systematic biases (i.e., compositional bias, long-branch attraction, heterotachy), leading to statistical inconsistency in phylogenetic reconstruction [ 4 – 7 ]. Phylogenomic data sets – using genome sequences to study evolutionary relationship – provide the best solution to these problems [ 1 , 8 ]. This approach requires compilation of large data sets that include many independent nuclear loci for many species [ 9 – 14 ]. Such data sets are less likely to succumb to sampling and systematic errors [ 13 ] by offering the possibility of analyzing large numbers of phylogenetically informative characters from different genomic locations, and also of corroborating phylogenetic results by varying the species sampled. If any systematic bias may be present in a fraction of individual loci sampled, it is unlikely that all affected loci will be biased in the same direction. Powerful analytical approaches that accommodate model heterogeneity among data partitions are becoming available to efficiently analyze such complex phylogenomic data sets [ 15 , 16 ].

Constructing phylogenomic data sets for large number of taxa still is, however, quite challenging. Most attempts to use this approach have been based either on few available complete genomic sequence data [ 13 , 17 , 18 ], or cDNA and ESTs sequences [ 9 , 12 , 18 , 19 ] for relatively few taxa. Availability of complete genomes limits the number of taxa that can be analyzed [ 13 , 17 ], imposing known problems for phylogenetic inference associated with poor taxon sampling [ 20 , 21 ]. On the other hand, methods based on ESTs or cDNA sequence data are not practical for many taxa because they require construction of cDNA libraries and fresh tissue samples. In addition, some genes may not be expressed in certain tissues or developmental stages, leading to cases with undesirable amounts of missing data [ 9 ]. The most efficient way to collect nuclear gene sequences for many taxa is to directly amplify target sequences using "universal" PCR primers, an approach so far used for just a few widely-used nuclear genes [ 22 – 25 ], or selected taxonomic groups (e.g., placental mammals and land plants). Widespread use of this strategy in most taxonomic groups has been hindered by the paucity of available PCR-targeted gene markers.

Mining genomic data to obtain candidate phylogenetic markers requires stringent criteria, since not all loci are likely to carry the appropriate historical signal. The phylogenetic informativeness of characters has been extensively debated on theoretical grounds [ 26 , 27 ], as well as in empirical cases [ 28 – 30 ]. Our study does not intend to contribute to this debate, but rather to focus on the practical issues involved in obtaining the raw data for analysis. What is the best strategy to select a few hundreds candidate loci from thousands of genes present in the genome? For practical purposes, a good phylogenetic nuclear gene marker must satisfy three criteria. First, orthologous genes should be easy to identify and amplify in all taxa of interest. One of the main problems associated with nuclear protein-coding genes used to infer phylogeny is uncertainty about their orthology [ 3 ]. This is especially true when multiple copies of a target gene are amplified by PCR from whole genomic DNA. To minimize the chance of sampling paralogous genes among taxa (the trap of "mistaken paralogy" that will lead to gene-tree-species-tree discordance), our approach is initiated by searches for single-copy nuclear genes in genomic databases. Under this criterion, even if gene duplication events may have occurred during evolution of the taxa of interest (e.g., the fish-specific whole-genome duplication event) [ 31 , 32 ], duplicated copies of a single-copy nuclear gene tend to be lost quickly, possibly due to dosage compensation [ 33 ]. Some authors estimate that almost 80% of the paralogs have been secondarily lost following the genome-duplication event [ 34 , 35 ]. Thus, if duplicated copies are lost before the relevant speciation events occur (Figure 1a, b ), no paralogous gene copies would be sampled. If the alternative situation occurs (Figure 1c ), paralogy will mislead phylogenetic inference resulting in topological discordance among genes. In the latter case, the topological distribution of this discordance may be used to reconstruct putative duplication/extinction events and clarify the putative mistaken paralogy [ 36 ]. The second criterion used to facilitate efficient data collection is to identify protein-coding genes with long exons (longer than a practical threshold determined by current DNA sequencing technology, for example 800 bp). Most genes are fragmented into small exons and large introns. For high taxonomic-level phylogenetic inference (deep phylogeny), intron sequences evolve too fast and are usually not informative, becoming an obstacle for the amplification and sequencing of more informative exon-coding sequences. The third criterion used seeks to identify reasonably conserved genes. Genes with low rates of evolution are less prone to accumulate homoplasy, and also provide the practical advantage of facilitating the design of universal primers for PCR that will work on a diversity of taxa. Furthermore, conserved protein-coding genes also are easy to align for analysis, based on their amino acid sequence.

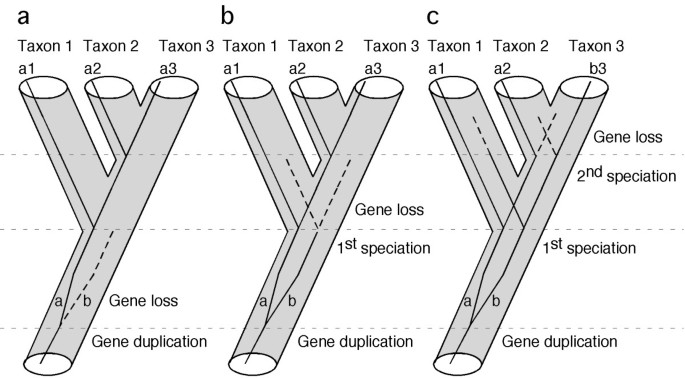
Single-copy genes are useful markers for phylogeny inference . Gene duplication and subsequent loss may not cause incongruence between gene tree and species tree if gene loss occurs before the first speciation event (a), or before the second speciation event (b). The only case that would cause incongruence is when the gene survived both speciation events and is asymmetrically lost in taxon 2 and taxon 3 (c).

Sequence conservatism and long exonic regions have been used as preferred criteria to select phylogenetic markers in the past [ 37 ]. However, finding many preferred, easy-to-apply gene markers is unlikely when candidate genes are manually screened from data bases or taken from isolated studies of few individual genes. This complexity partially explains the scarcity of currently available nuclear gene markers in many taxonomic groups. To address the problem, we present a simple bioinformatic approach to obtain nuclear gene markers from complete genomic data, based on the three aforementioned criteria. Our method incorporates two improvements over the traditional way of manually picking genes and testing their phylogenetic utilities. These improvements include using full genomic information and automating the process of searching for candidate makers. We apply the method to Actinoptertygii (ray-finned fish), the largest vertebrate clade – they make up about half of all known vertebrate species – with a poorly known phylogeny [ 38 – 42 ]. We also present experimental tests to show that PCR primers designed for a subset of the candidate markers can efficiently amplify these markers for a highly diverse sample of ray-finned fishes. Comparative analyses of the sequences obtained show encouraging phylogenetic properties for future studies.

The bioinformatic pipeline used is shown in Figure 2 . Within-genome sequence comparisons resulted in 2,797 putative single-copy exons (> 800 bp) in zebrafish ( D. rerio ), and 1,822 in torafugu ( T. rubripes ), 2132 in stickleback ( G. aculeatus ), and 1809 in Japanese rice fish ( O. latipes ). Note that our operational definition of a "single-copy" gene only requires that the fragment is not present as a second copy in the genome with similarity higher than 50%. Some single-copy genes may, in fact, have duplicates in the genome that are less than 50% similar. Pairwise between-genome comparisons of the single-copy exon sequences resulted in a range of 113 to 281 putative orthologs shared among genomes, that have similarity greater than 70%. The lowest number of "conserved orthologs" was detected between zebrafish and rice fish, and the highest between torafugu and stickleback. The number of putative conserved orthologs shared among three or more genomes varied from case to case; for example, it peaked at 155 when comparing torafugu, Japanese rice fish, and stickleback, but only 61 for the comparison involving torafugu, Japanese ricefish, and zebrafish. All the information resulting from these analyses is publicly available in our website [ 43 ], and a sample output of candidate markers is shown in Additional file 1 .

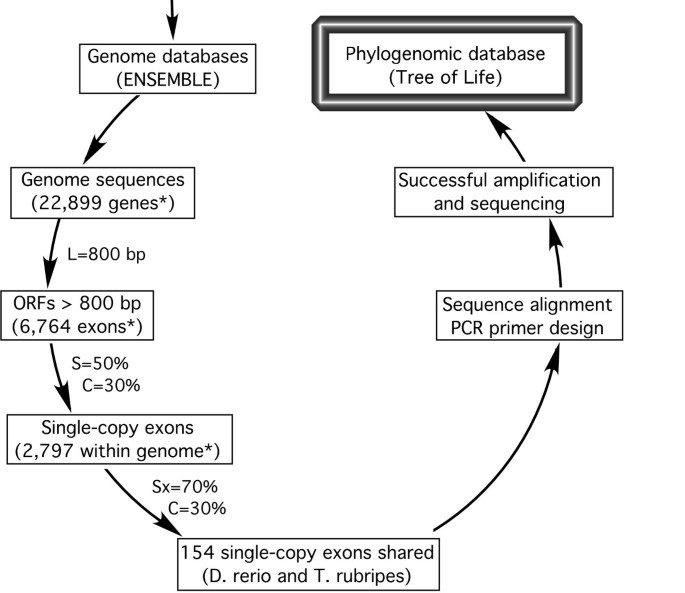
The bioinformatic pipeline for phylogenetic markers development . It involves within- and across-genome sequences comparison, in silico test with sequences in other species, and experimental validation. Numbers of genes and exons identified for D. rerio are indicated by the asterisk. Exon length (L), within-genome similarity (S), between-genome similarity (Sx), and coverage (C) are adjustable parameters (see methods).

To investigate the properties of candidate markers, we analyzed those found in the zebrafish and torafugu comparison, since their genome sequences are well annotated. Among them, 154 putative homologs were identified between zebrafish and torafugu by cross-genome comparison. Further comparison with EST sequences from other fish species reduced this number to 138 candidate markers (Supplementary Table 1). The 154 candidate markers shared between these two genomes according to our search criteria are distributed among 24 of the 25 chromosomes of zebrafish, and a Chi-square test did not reject a Poisson distribution of markers among chromosomes (χ 2 = 16.99, df = 10, p = 0.0746). The size of candidate markers ranged from 802 to 5811 bp (in D. rerio ). Their GC content ranged from 41.6% to 63.9% (in D. rerio ), and the average similarity of the DNA sequence of these markers between D. rerio and T. rubripes varied from 77.3% to 93.2% (constrained by the search criteria).

To test the practical value of potential phylogenetic markers, 15 gene fragments were randomly picked from the candidate list of 154 and tested experimentally on 36 taxa, chosen to represent two-thirds of all ray-finned fish orders (see Additional file 2 ). PCR primers were designed on conserved flanking regions for each fragment, based on the genomic sequences and tested on all taxa (Table 1 ). Ten out of the 15 markers examined successfully amplified a single product of the predicted size by a nested PCR approach in 31 taxa. For comparative sequence analyses, we took only 14 taxa ( Amia calva , D. rerio , Semotilus atromaculatus , Ictalurus punctatus , Oncorhynchus mykiss , Brotula multibarbata , Fundulus heteroclitus , Oryzias latipes , Oreochromis niloticus , Gasterosteus aculeatus , Lycodes atlanticus , T. rubripes , Morone chrysops , Lutjanus mahogoni ) that could be amplified and sequenced directly for the set of 10 markers [GenBank: EF032909 – EF033038]. The size of the sequenced fragments ranged from 666 to 987 bp, and the average uncorrected genetic distances for DNA sequence of the 10 markers among the 14 taxa ranged from 13% to 21%. We present (Table 2 ) additional characteristics of the data set such as the substitution rate, consistency index (CI), gamma shape parameter (α), relative composition variability (RCV), and treeness [ 44 ] resulting from phylogenetic analysis of the sequences of the 10 new markers. Values obtained are similar to those observed in a commonly used phylogenetic marker – recombination activating gene 1 (RAG-1, Table 2 ). For the newly characterized phylogenetic markers, the substitution rate is negatively correlated with CI (r = -0.84, P = 0.0026) and marginally correlated with α (r = -0.56, P = 0.095). In contrast, base composition heterogeneity (RCV) and the phylogenetic signal to noise index (treeness index) are not correlated with substitution rate. Based on the treeness value, genes ENC1, plagl2, Ptr, Gylt and tbr1 seem well suited for phylogenetic studies at high taxonomic level among ray-finned fishes.

A phylogeny of the 14 taxa using concatenated sequences of all 10 markers (total of 7,872 bp) was inferred on the basis of protein and DNA sequences. For the protein sequence data, a JTT model with gamma parameter accounting for rate heterogeneity was selected by ProtTest [ 45 ]. The data were partitioned by gene, as this strategy was favoured by the Akaike information criterion (AIC) over treating the concatenated sequences as a single partition. Maximum likelihood (ML) and Bayesian analysis (BA) resulted in the same tree (Figure 3a ). A similar topology to Figure 3a was obtained by ML analysis of nucleotide sequences with RY-coded nucleotides to address potential artefacts due to base compositional bias [ 44 ]. The positions of Brotula and Morone remain somewhat unresolved, receiving low bootstrap support and conflicting resolution based on either protein or RY-coded nucleotide data. When analyzed separately, all individual gene trees display low support in many branches and none of them has the same topology as the "total evidence" tree based on all 10 genes (see Additional file 3 ). However, only 6 individual genes exhibit significant differences with the total evidence tree (based on one tailed SH tests with p < 0.05), the exceptions being myh6 (p = 0.113), Gylt (p = 0.091), plagl2 (p = 0.056)), and sreb2 (p = 0.080).

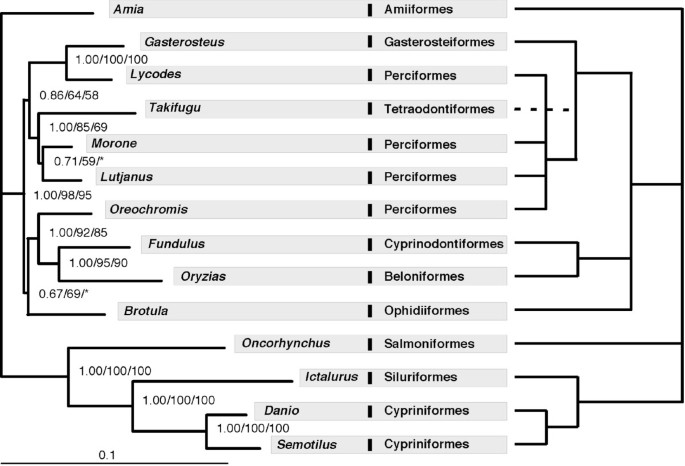
A comparison of the maximum likelihood phylogram inferred in this study with the conventional phylogeny . (a) Left panel – the phylogram of 14 taxa inferred from protein sequences of 10 genes; (b) right panel – a "consensus" phylogeny following Nelson [50]. The numbers on the branches are Bayesian posterior probability, ML bootstrap values estimated from protein sequences and ML bootstrap values estimated from RY-coded nucleotide sequence. Asterisks indicate bootstrap supports less than 50.

The bioinformatic approach implemented in this study resulted in a large set (154 loci for the zebrafish and torafugu comparison) of candidate genes to infer high-level phylogeny of ray-finned fishes. The actual number of candidate loci depended on the genomes being compared and the fixed search parameters. Experimental tests of a smaller subset (15 loci) demonstrate that a large fraction (2/3) of these candidates are easily amplified by PCR from whole genomic DNA extractions in a vast diversity of fish taxa. The assumption that these loci are represented by a single copy in the fish genomes could not be rejected by the PCR assays in the species tested (all amplifications resulted in a single product), increasing the likelihood that the genetic markers are orthologous and suitable to infer organismal phylogeny. Our method is based on searching, under specific criteria, the available complete genomic databases of organisms closely related to the taxa of interest. Therefore, the same approach that is shown to be successful for fishes could be applied to other groups of organisms for which two or more complete genome sequences exist. Parameter values (L, S, and C) used for the search (Figure 2 ) may be altered to obtain fragments of different size or with different levels of conservation (i.e., less conserved for phylogenies of more closely related organisms).

An alternative way to develop nuclear gene markers for phylogenetic studies is to construct a cDNA library or sequence several ESTs for a small pilot group of taxa, and then to design specific PCR primers to amplify the orthologous gene copy in all the other taxa of interest [ 19 , 46 ]. The major potential problem with this approach stems from the fact that the method starts with a cDNA library or a set of EST sequences, with no prior knowledge of how many copies a gene has in each genome. As discussed above, this condition may lead to mistaken paralogy. In our approach, we search the genomic database to find single-copy candidates so no duplicate gene copies, if present, would be missed (see below).

Recent studies have proposed whole genome duplication events during vertebrate evolution and also genome duplications restricted to ray-finned fishes [ 31 , 32 , 47 , 48 ]. Our results indicate that many single-copy genes still exist in a wide diversity of fish taxa (representing 28 orders of actinopterygian fishes), in agreement with previous estimates that a vast majority of duplicated genes are secondarily lost [ 34 , 35 ]. All 154 candidates were identified as single-copy genes in D. rerio and T. rubripes , according to our search criteria. Our results also show the 154 candidate genes are randomly distributed in the fish genome (at least among chromosomes of D. rerio ). In the experimental tests, 10 out of 15 markers were found in single-copy condition in all successful amplifications, including the tetraploid species, O. mykiss . However, relaxing the search criteria, and conserving targets less than 50% similar in a subsequent blast search against the zebrafish genome, 7 of the 10 genes were found to have "alignable paralogs" (the 3 exceptions were myh6, tbr1, and Gylt). Genomes of medaka, stickleback, and fugu were also checked for these 3 genes, and no "paralogs" were detected, suggesting the sequences of ray-finned fish collected for these 3 genes are unambiguously orthologous to each other. Phylogenetic analyses for each of the 7 genes that include the putative paralogs found by this procedure produced tree topologies that strongly suggest an ancient duplication event in the vertebrate lineage, before the divergence of tetrapods from ray-finned fishes. Paralogous sequences are placed at the base of the tetrapod-actinopteryigian divergence, or as part of a basal polytomy with the other tetrapod and ray-finned fish sequences. In the terminology proposed by Remm et al. [ 49 ] these would be considered out-paralogs. In no case are these sequences nested among ingroup actinopterygian sequences (see Additional file 4 ), as would be the case expected for in-paralogs [ 49 ]. Stringent search critera implemented in our approach followed by phylogenetic analysis can distinguish between orthologs and putative our-paralogs. Although the method will not guarantee that single copy genes amplified by PCR in several taxa are orthologs as opposed to in-paralogs, the existence and identification of genome-scale single-copy nuclear markers should facilitate the construction of the tree of life, even if the evolutionary mechanism responsible for maintaining single-copy genes is poorly known [ 33 ].

The molecular evolutionary profiles of the 10 newly developed markers are in the same range as RAG-1, a widely-used gene marker in vertebrates. The genes with high treeness values have intermediate substitution rate, suggesting that optimal rate and base composition stationarity are important factors that determine the suitability of a phylogenetic marker. The phylogeny based on individual markers revealed incongruent phylogenetic signal among 6 of the 10 individual genes. This incongruence suggests that significant biases in the data might obscure the true phylogenetic signal in some individual genes, but the direction of the bias is hardly shared among genes (Additional file 3 ), justifying the use of genome-scale gene makers to infer organismal phylogeny.

Finally, with respect to the phylogenetic results per se , there are two significant areas of discrepancy between the phylogeny obtained in this study (Figure 3a ) and a consensus view of fish phylogeny (Figure 3b ) [ 50 ]. Although these differences could be due to poor taxonomic sampling, we discuss them briefly. First, the traditional tree groups cichlids with other perciforms, whereas our results showed the cichlid O. niloticus is more closely related to atherinomorphs (Cyprinodontiformes + Beloniformes) than to other perciforms. This result also was supported by two recent studies analysing multiple nuclear genes [ 17 , 51 ]. The second difference is that the traditional tree groups Lycodes with other perciforms, while Lycodes was found closely related to Gasterosteus (Gasterosteiformes) in our results. Interestingly, the sister-taxa relationship between Lycodes and Gasterosteus also is supported by recent studies using mitochondrial genome data [ 38 , 52 ]. The difference between our "total evidence" tree and the classical hypothesis is significant based on the new data, as indicated by a one-tailed Shimodaira-Hasegawa (SH) test (p = 0.000) [ 53 ].

We developed a genome-based approach to identify nuclear gene markers for phylogeny inference that are single-copy, contain large exons, and are conserved across extensive taxonomic distances. We show that our approach has practical value through direct experimentation on a representative sample of ray-finned fish, the largest vertebrate clade in need of phylogenetic resolution. The same approach, however, could be applied to other groups of organisms as long as two or more complete genome sequences are available. This research may have important implications for assembling the tree of life.

Genome-scale mining for phylogenetic markers

Whole genomic sequences of Danio rerio and Takifugu rubripes were retrieved from the ENSEMBL database [ 54 ]. Exon sequences with length > 800 bp were then extracted from the genome databases. The exons extracted were compared in two steps: (1) within-genome sequence comparisons and (2) between genome comparisons. The first step is designed to generate a set of single-copy nuclear gene exons (length > 800 bp) within each genome, whereas the second step should identify single-copy, putatively orthologous exons between D. rerio and T. rubripes (Figure 2 ). The BLAST algorithm was used for sequence similarity comparison. In addition to the parameters available in the BLAST program, we applied another parameter, coverage (C), to identify global sequence similarity between exons. The coverage was defined as the ratio of total length of locally aligned sequences over the length of query sequence. The similarity (S) was set to S < 50% for within-genome comparison, which means that only genes that have no counterpart more than 50% similar to themselves were kept. The similarity was set to S × > 70% and the coverage was set to C > 30% in cross-genome comparison, which selected genes that are 70% similar and 30% aligned between D. rerio and T. rubripes . Subsequent comparisons were performed on the newly available genome of stickleback ( Gasterosteus aculeatus ) and Japanese rice fish ( Oryzias latipes ), as described above. We programmed this procedure using PERL programming language to automate the processes and made the source code publicly available on our website [ 43 ]. We are in progress to make it available for other genomic sequences and parameter values.

Experimental testing for candidate markers

PCR and sequencing primers were designed on aligned sequences of D. rerio and T. rubripes for 15 random selected genes. Primer3 was used to design the primers [ 55 ]. Degenerate primers and a nested-PCR design were used to assure the amplification for each gene in most of the taxa. Ten of the 15 genes tested were amplified with single fragment in most of the 36 taxa examined. PCR primers for 10 gene markers are listed in Table 1 . The amplified fragments were directly sequenced, without cloning, using the BigDye system (Applied Biosystems). Sequences of the frequently used RAG1 gene were retrieved for the same taxa from GenBank for comparison to the newly developed markers [GenBank: AY430199, NM_131389, U15663, AB120889, DQ492511, AY308767, AF108420, EF033039 – EF033043]. When RAG1 sequences for the same taxa were not available, a taxon of the same family was used, i.e. Nimbochromis was used instead of Oreochromis and Neobythites was used instead of Brotula .

Phylogenetic analysis

Sequences of the 10 new markers in the 14 taxa were used in phylogenetic analysis to assess their performance. Sequences were aligned using ClustalX [ 56 ] on the translated protein sequences. Uncorrected genetic distances were calculated using PAUP [ 57 ]. Relative substitution rate for each markers were estimated using a Bayesian approach [ 58 ]. Relative composition variability (RCV) and treeness were calculated following Phillips and Penny [ 44 ]. Prottest [ 45 ] was used to chose the best model for protein sequence data and the AIC criteria to determine the scheme of data partitioning. Bayesian analysis implemented in MrBayes v3.1.1 and maximum likelihood analysis implemented in TreeFinder [ 59 ] were performed on the protein sequences. One million generation with 4 chains were run for Bayesian analysis and the trees sampled prior to reaching convergence were discarded (as burnin) before computing the consensus tree and posterior probabilities. Two independent runs were used to provide additional confirmation of convergence of posterior probability distribution. Given the biased base composition in the nucleotide data indicated by the RCV value (Table 2 ), we analyzed the nucleotide data under the RY-coding scheme (C and T = Y, A and G = R), partitioned by gene in TreeFinder, since RY-coded data are less sensitive to base compositional bias [ 44 ]. Alternative hypotheses were tested by one-tailed Shimodaira and Hasegawa (SH) test [ 53 ] with 1000 RELL bootstrap replicates implemented in TreeFinder.

Delsuc F, Brinkmann H, Philippe H: Phylogenomics and the reconstruction of the tree of life. Nat Rev Genet. 2005, 6 (5): 361-375. 10.1038/nrg1603.

Article   CAS   PubMed   Google Scholar  

Pamilo P, Nei M: Relationships Between Gene Trees and Species Trees. Mol Biol Evol. 1988, 5 (5): 568-583.

CAS   PubMed   Google Scholar  

Fitch WM: Distinguishing homologous from analogous proteins. Syst Zool. 1970, 19 (2): 99-113. 10.2307/2412448.

Lopez P, Casane D, Philippe H: Heterotachy, an important process of protein evolution. Mol Biol Evol. 2002, 19 (1): 1-7.

Felsenstein J: Case in which parsimony or compatibility methods will be positively misleading. Syst Biol. 1978, 27: 401-410.

Article   Google Scholar  

Weisburg WG, Giovannoni SJ, Woese CR: The Deinococcus-Thermus phylum and the effect of rRNA composition on phylogenetic tree construction. Syst Appl Microbiol. 1989, 11: 128-134.

Foster PG, Hickey DA: Compositional bias may affect both DNA-based and protein-based phylogenetic reconstructions. J Mol Evol. 1999, 48 (3): 284-290. 10.1007/PL00006471.

Eisen JA, Fraser CM: Phylogenomics: intersection of evolution and genomics. Science. 2003, 300 (5626): 1706-1707. 10.1126/science.1086292.

Philippe H, Snell EA, Bapteste E, Lopez P, Holland PW, Casane D: Phylogenomics of eukaryotes: impact of missing data on large alignments. Mol Biol Evol. 2004, 21 (9): 1740-1752. 10.1093/molbev/msh182.

Driskell AC, Ane C, Burleigh JG, McMahon MM, O'Meara B C, Sanderson MJ: Prospects for building the tree of life from large sequence databases. Science. 2004, 306 (5699): 1172-1174. 10.1126/science.1102036.

Takezaki N, Figueroa F, Zaleska-Rutczynska Z, Klein J: Molecular phylogeny of early vertebrates: monophyly of the agnathans as revealed by sequences of 35 genes. Mol Biol Evol. 2003, 20 (2): 287-292. 10.1093/molbev/msg040.

Bapteste E, Brinkmann H, Lee JA, Moore DV, Sensen CW, Gordon P, Durufle L, Gaasterland T, Lopez P, Muller M, Philippe H: The analysis of 100 genes supports the grouping of three highly divergent amoebae: Dictyostelium, Entamoeba, and Mastigamoeba. Proc Natl Acad Sci U S A. 2002, 99 (3): 1414-1419. 10.1073/pnas.032662799.

Article   PubMed Central   CAS   PubMed   Google Scholar  

Rokas A, Williams BL, King N, Carroll SB: Genome-scale approaches to resolving incongruence in molecular phylogenies. Nature. 2003, 425 (6960): 798-804. 10.1038/nature02053.

Murphy WJ, Eizirik E, Johnson WE, Zhang YP, Ryder OA, O'Brien SJ: Molecular phylogenetics and the origins of placental mammals. Nature. 2001, 409 (6820): 614-618. 10.1038/35054550.

Brandley MC, Schmitz A, Reeder TW: Partitioned Bayesian analyses, partition choice, and the phylogenetic relationships of scincid lizards. Syst Biol. 2005, 54 (3): 373-390. 10.1080/10635150590946808.

Article   PubMed   Google Scholar  

Castoe TA, Doan TM, Parkinson CL: Data partitions and complex models in Bayesian analysis: the phylogeny of Gymnophthalmid lizards. Syst Biol. 2004, 53 (3): 448-469. 10.1080/10635150490445797.

Chen WJ, Ortí G, Meyer A: Novel evolutionary relationship among four fish model systems. Trends Genet. 2004, 20 (9): 424-431. 10.1016/j.tig.2004.07.005.

Rokas A, Kruger D, Carroll SB: Animal evolution and the molecular signature of radiations compressed in time. Science. 2005, 310 (5756): 1933-1938. 10.1126/science.1116759.

Whittall JB, Medina-Marino A, Zimmer EA, Hodges SA: Generating single-copy nuclear gene data for a recent adaptive radiation. Mol Phylogenet Evol. 2006, 39 (1): 124-134. 10.1016/j.ympev.2005.10.010.

Hillis DM, Pollock DD, McGuire JA, Zwickl DJ: Is sparse taxon sampling a problem for phylogenetic inference?. Syst Biol. 2003, 52 (1): 124-126. 10.1080/10635150390132911.

Article   PubMed Central   PubMed   Google Scholar  

Soltis DE, Albert VA, Savolainen V, Hilu K, Qiu YL, Chase MW, Farris JS, Stefanovic S, Rice DW, Palmer JD, Soltis PS: Genome-scale data, angiosperm relationships, and "ending incongruence": a cautionary tale in phylogenetics. Trends Plant Sci. 2004, 9 (10): 477-483. 10.1016/j.tplants.2004.08.008.

Lovejoy NR, Collette BB: Phylogenetic relaionships of new world needlefishes (Teleostei: Belonidae) and the biogeography of transitions between marine and freshwater habitats. Copeia. 2001, 2001 (2): 324-338. 10.1643/0045-8511(2001)001[0324:PRONWN]2.0.CO;2.

Saint KM, Austin CC, Donnellan SC, Hutchinson MN: C-mos, a nuclear marker useful for squamate phylogenetic analysis. Mol Phylogenet Evol. 1998, 10 (2): 259-263. 10.1006/mpev.1998.0515.

Mohammad-Ali K, Eladari ME, Galibert F: Gorilla and orangutan c-myc nucleotide sequences: inference on hominoid phylogeny. J Mol Evol. 1995, 41 (3): 262-276. 10.1007/BF01215173.

Groth JG, Barrowclough GF: Basal divergences in birds and the phylogenetic utility of the nuclear RAG-1 gene. Mol Phylogenet Evol. 1999, 12 (2): 115-123. 10.1006/mpev.1998.0603.

Lyons-Weiler J, Hoelzer GA, Tausch RJ: Relative apparent synapomorphy analysis (RASA). I: The statistical measurement of phylogenetic signal. Mol Biol Evol. 1996, 13 (6): 749-757.

Philippe H, Zhou Y, Brinkmann H, Rodrigue N, Delsuc F: Heterotachy and long-branch attraction in phylogenetics. BMC Evol Biol. 2005, 5: 50-10.1186/1471-2148-5-50.

Collins TM, Fedrigo O, Naylor GJ: Choosing the best genes for the job: the case for stationary genes in genome-scale phylogenetics. Syst Biol. 2005, 54 (3): 493-500. 10.1080/10635150590947339.

Steel MA, Lockhart PJ, Penny D: Confidence in evolutionary trees from biological sequence data. Nature. 1993, 364 (6436): 440-442. 10.1038/364440a0.

Phillips MJ, Delsuc F, Penny D: Genome-scale phylogeny and the detection of systematic biases. Mol Biol Evol. 2004, 21 (7): 1455-1458. 10.1093/molbev/msh137.

Amores A, Force A, Yan YL, Joly L, Amemiya C, Fritz A, Ho RK, Langeland J, Prince V, Wang YL, Westerfield M, Ekker M, Postlethwait JH: Zebrafish hox clusters and vertebrate genome evolution. Science. 1998, 282 (5394): 1711-1714. 10.1126/science.282.5394.1711.

Meyer A, Van de Peer Y: From 2R to 3R: evidence for a fish-specific genome duplication (FSGD). Bioessays. 2005, 27 (9): 937-945. 10.1002/bies.20293.

Ciccarelli FD, von Mering C, Suyama M, Harrington ED, Izaurralde E, Bork P: Complex genomic rearrangements lead to novel primate gene function. Genome Res. 2005, 15 (3): 343-351. 10.1101/gr.3266405.

Woods IG, Wilson C, Friedlander B, Chang P, Reyes DK, Nix R, Kelly PD, Chu F, Postlethwait JH, Talbot WS: The zebrafish gene map defines ancestral vertebrate chromosomes. Genome Res. 2005, 15 (9): 1307-1314. 10.1101/gr.4134305.

Jaillon O, Aury JM, Brunet F, Petit JL, Stange-Thomann N, Mauceli E, Bouneau L, Fischer C, Ozouf-Costaz C, Bernot A, Nicaud S, Jaffe D, Fisher S, Lutfalla G, Dossat C, Segurens B, Dasilva C, Salanoubat M, Levy M, Boudet N, Castellano S, Anthouard V, Jubin C, Castelli V, Katinka M, Vacherie B, Biemont C, Skalli Z, Cattolico L, Poulain J, De Berardinis V, Cruaud C, Duprat S, Brottier P, Coutanceau JP, Gouzy J, Parra G, Lardier G, Chapple C, McKernan KJ, McEwan P, Bosak S, Kellis M, Volff JN, Guigo R, Zody MC, Mesirov J, Lindblad-Toh K, Birren B, Nusbaum C, Kahn D, Robinson-Rechavi M, Laudet V, Schachter V, Quetier F, Saurin W, Scarpelli C, Wincker P, Lander ES, Weissenbach J, Roest Crollius H: Genome duplication in the teleost fish Tetraodon nigroviridis reveals the early vertebrate proto-karyotype. Nature. 2004, 431 (7011): 946-957. 10.1038/nature03025.

Page RD, Cotton JA: Vertebrate phylogenomics: reconciled trees and gene duplications. Pac Symp Biocomput. 2002, 536-547.

Google Scholar  

Friedlander TP, Regier JC, Mitter C: Nuclear gene sequences for higher level phylogenetic analysis: 14 promising candidates. Syst Biol. 1992, 41 (4): 483-490. 10.2307/2992589.

Miya M, Takeshima H, Endo H, Ishiguro NB, Inoue JG, Mukai T, Satoh TP, Yamaguchi M, Kawaguchi A, Mabuchi K, Shirai SM, Nishida M: Major patterns of higher teleostean phylogenies: a new perspective based on 100 complete mitochondrial DNA sequences. Mol Phylogenet Evol. 2003, 26 (1): 121-138. 10.1016/S1055-7903(02)00332-9.

Stiassny MLJ, Wiley EO, Johnson GD, de Carvalho MR: Gnathostome fishes. Assembling The Tree of Life. Edited by: Cracraft J, Donoghue MJ. 2004, New York , Oxford University Press, 410-429.

Stiassny MLJ, Parenti LR, Johnson GD: Interrelationships of fishes. 1996, San Diego , Academic Press, xiii, 496 p.-

Arratia G: Phylogenetic relationships of teleostei: past and present. Estud Oceanol. 2000, 19: 19-51.

Greenwood PH, Miles RS, Patterson C: Interrelationships of fishes. 1973, London , Academic Press, 536 p.-

Phylomarker - mining phylogenetic markers for assembling the Tree of Life [http://bioinfo-srv1.awh.unomaha.edu/phylomarker].

Phillips MJ, Penny D: The root of the mammalian tree inferred from whole mitochondrial genomes. Mol Phylogenet Evol. 2003, 28 (2): 171-185. 10.1016/S1055-7903(03)00057-5.

Abascal F, Zardoya R, Posada D: ProtTest: selection of best-fit models of protein evolution. Bioinformatics. 2005, 21 (9): 2104-2105. 10.1093/bioinformatics/bti263.

Small RL, Cronn RC, Wendel JF: L. A. S. Johnson Review No. 2. Use of nuclear genes for phylogeny reconstruction in plants. Australian Systematic Botany. 2004, 17: 145-170. 10.1071/SB03015.

Article   CAS   Google Scholar  

Taylor JS, Braasch I, Frickey T, Meyer A, Van de Peer Y: Genome duplication, a trait shared by 22000 species of ray-finned fish. Genome Res. 2003, 13 (3): 382-390. 10.1101/gr.640303.

Van de Peer Y, Taylor JS, Meyer A: Are all fishes ancient polyploids?. J Struct Funct Genomics. 2003, 3 (1-4): 65-73. 10.1023/A:1022652814749.

Remm M, Storm CE, Sonnhammer EL: Automatic clustering of orthologs and in-paralogs from pairwise species comparisons. J Mol Biol. 2001, 314 (5): 1041-1052. 10.1006/jmbi.2000.5197.

Nelson JS: Fishes of the world. 2006, New York , John Wiley and Sons, Inc., 601 pp.-4th

Steinke D, Salzburger W, Meyer A: Novel Relationships Among Ten Fish Model Species Revealed Based on a Phylogenomic Analysis Using ESTs. J Mol Evol. 2006, 62 (6): 772-784. 10.1007/s00239-005-0170-8.

Miya M, Satoh TP, Nishida M: The phylogenetic position of toadfishes (order Batrachoidiformes) in the higher ray-finned fish as inferred from partitioned Bayesian analysis of 102 whole mitochondrial genome sequences. Biol J Linn Sco Lond. 2005, 85: 289-306. 10.1111/j.1095-8312.2005.00483.x.

Shimodaira H, Hasegawa M: Multiple comparisons of log-likelihoods with applications to phylogenetic inference. Mol Biol Evol. 1999, 16: 1114-1116.

Ensembl [www.ensembl.org/index.html].

Rozen S, Skaletsky H: Primer3 on the WWW for general users and for biologist programmers. Methods Mol Biol. 2000, 132: 365-386.

Thompson JD, Gibson TJ, Plewniak F, Jeanmougin F, Higgins DG: The CLUSTAL_X windows interface: flexible strategies for multiple sequence alignment aided by quality analysis tools. Nucleic Acids Res. 1997, 25 (24): 4876-4882. 10.1093/nar/25.24.4876.

Swofford DL: PAUP*. Phylogenetic Analysis Using Parsimony (*and Other Methods). Version 4. 2003, Sinauer Associates, Sunderland, Massachusetts.

Ronquist F, Huelsenbeck JP: MrBayes 3: Bayesian phylogenetic inference under mixed models. Bioinformatics. 2003, 19 (12): 1572-1574. 10.1093/bioinformatics/btg180.

Jobb G, von Haeseler A, Strimmer K: TREEFINDER: a powerful graphical analysis environment for molecular phylogenetics. BMC Evol Biol. 2004, 4: 18-10.1186/1471-2148-4-18.

Download references

Acknowledgements

This work was supported by the grants from University of Nebraska-Lincoln (to C. L.), National Science Foundation DEB-9985045 (to G. O.) and University of Nebraska-Omaha (to G. L.). We thank Fred J. Potmesil and Thaine W. Rowley for help in computer programming.

Author information

Authors and affiliations.

School of Biological Sciences, University of Nebraska, Lincoln, NE, 68588, USA

Chenhong Li & Guillermo Ortí

Department of Mathematics, University of Nebraska, Omaha, NE, 68182, USA

Department of Biology, University of Nebraska, Omaha, NE, 68182, USA

You can also search for this author in PubMed   Google Scholar

Corresponding authors

Correspondence to Chenhong Li or Guoqing Lu .

Additional information

Authors' contributions.

CL conceived of the study, designed the bioinformatic pipeline, carried out the experimental tests, and drafted the manuscript. GO conceived of the study and helped to draft the manuscript. GZ implemented the bioinformatics pipeline and developed the web pages. GL conceived of the study, designed the bioinformatics pipeline and the web pages, and helped to draft the manuscript. All authors have read and approved the final manuscript.

Electronic supplementary material

12862_2006_338_moesm1_esm.rtf.

Additional file 1: Exon ID, exon length, GC content of predicted single nuclear gene markers in zebrafish and torafugu, as well the blast result between orthologous genes. (RTF 249 KB)

Additional file 2: Results of PCR amplification of 10 new makers in 36 species of ray-finned fishes. (RTF 165 KB)

12862_2006_338_moesm3_esm.pdf.

Additional file 3: Maximum likelihood phylogeny based on protein sequences of individual genes, zic1, myh6, RYR3, Ptr, tbr1, ENC1, Gylt, SH3PX3, plagl2, and sreb2. Bootstrap value higher than 50% were mapped on branches. (PDF 7 KB)

12862_2006_338_MOESM4_ESM.pdf

Additional file 4: ML phylogenies based on protein sequences of individual genes and their out-paralogs found by relaxing our search criteria to include fragments with similarity < 50%. (PDF 9 KB)

Authors’ original submitted files for images

Below are the links to the authors’ original submitted files for images.

Authors’ original file for figure 1

Authors’ original file for figure 2, authors’ original file for figure 3, rights and permissions.

This article is published under license to BioMed Central Ltd. This is an Open Access article distributed under the terms of the Creative Commons Attribution License ( http://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Reprints and permissions

About this article

Cite this article.

Li, C., Ortí, G., Zhang, G. et al. A practical approach to phylogenomics: the phylogeny of ray-finned fish (Actinopterygii) as a case study. BMC Evol Biol 7 , 44 (2007). https://doi.org/10.1186/1471-2148-7-44

Download citation

Received : 25 September 2006

Accepted : 20 March 2007

Published : 20 March 2007

DOI : https://doi.org/10.1186/1471-2148-7-44

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Candidate Marker
• Phylogenetic Marker
• Compositional Bias
• Phylogenetic Informativeness
• Organismal Phylogeny

BMC Ecology and Evolution

ISSN: 2730-7182

• General enquiries: [email protected]

An official website of the United States government

Official websites use .gov A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS A lock ( Lock Locked padlock icon ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

• Publications
• Account settings
• Advanced Search
• Journal List

Phylogenetic Analysis Guides Transporter Protein Deorphanization: A Case Study of the SLC25 Family of Mitochondrial Metabolite Transporters

Katie l byrne, richard v szeligowski, hongying shen.

• Author information
• Article notes
• Copyright and License information

Correspondence: [email protected]

Current address: Department of Environmental Science and Policy, University of California at Davis, Davis, CA 95616, USA.

Received 2023 Jul 20; Revised 2023 Aug 13; Accepted 2023 Aug 14; Collection date 2023 Sep.

Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( https://creativecommons.org/licenses/by/4.0/ ).

Homology search and phylogenetic analysis have commonly been used to annotate gene function, although they are prone to error. We hypothesize that the power of homology search in functional annotation depends on the coupling of sequence variation to functional diversification, and we herein focus on the S o L ute C arrier (SLC25) family of mitochondrial metabolite transporters to survey this coupling in a family-wide manner. The SLC25 family is the largest family of mitochondrial metabolite transporters in eukaryotes that translocate ligands of different chemical properties, ranging from nucleotides, amino acids, carboxylic acids and cofactors, presenting adequate experimentally validated functional diversification in ligand transport. Here, we combine phylogenetic analysis to profile SLC25 transporters across common eukaryotic model organisms, from Saccharomyces cerevisiae , Caenorhabditis elegans , Drosophila melanogaster , Danio rerio , to Homo sapiens , and assess their sequence adaptations to the transported ligands within individual subfamilies. Using several recently studied and poorly characterized SLC25 transporters, we discuss the potentials and limitations of phylogenetic analysis in guiding functional characterization.

Keywords: phylogenetic analysis, SLC25, mitochondria, metabolite transport, deorphanization

1. Introduction

It is estimated that at least 20–30% of the coding proteins derived from any model organism’s genome have poorly characterized functions [ 1 ]. To predict their functions, in silico analysis, especially sequence homology, is frequently used for functional annotation based on their characterized homologous proteins. However, this strategy is prone to false predictions due to functional diversification in protein evolution [ 2 ]. We therefore reasoned that the power of homology search in predicting function depends on the coupling of sequence variation to functional diversification, which can be evaluated by performing a phylogenetic analysis of homologs that span sufficient experimentally validated functional diversity.

In the context of cellular metabolism, specifically for metabolic enzymes and metabolite transporters of poorly characterized function, we consider functional prediction, the “deorphanization” effort, as predicting the ligands specifically binding at the evolutionarily conserved, putative catalytic pocket. This binding ligand can be a translocating ligand for a transporter, a substrate or product of a metabolic enzyme, or a regulatory molecule bound at the same pocket of these pseudogenized enzymes or transporters that gain additional moonlighting functions [ 3 ]. To test whether phylogenetic analysis is sufficient for guiding deorphanization and predicting putative ligands, we chose the mitochondrial SLC25 metabolite transporter family as the model family.

The SLC25 family is the largest protein family responsible for translocating metabolites across the mitochondrial inner membrane, a process that critically controls all aspects of mitochondrial physiology [ 4 , 5 , 6 , 7 , 8 ]. The human genome encodes 53 SLC25 genes, including four adenine nucleotide carriers (ADP/ATP carriers) that exchange ADP 3− for ATP 4− to support cellular bioenergetics and UCP1, which is exclusively expressed in brown adipose tissue and dissipates the proton motive force to generate heat. Despite their critical roles, at least one-third of human SLC25 transporters remain poorly characterized, leaving ample space for deorphanization efforts. Meanwhile, decades of elegant experimental studies have provided functional and mechanistic insights, presenting an ideal case for evaluating the coupling of sequence variation and functional diversification for proteins within the SLC25 family.

The SLC25 family is a prime candidate for our investigation into phylogenetic-analysis-guided studies for many reasons. First, the family is extraordinarily functionally diverse, being the largest protein family (53 in humans) that translocate a variety of chemically distinct metabolite ligands across the inner mitochondrial membrane, ranging from nucleotides to amino acids, carboxylic acids, inorganic ions, and different cofactors to protons with high specificity

Second, structure–function analysis, leveraging elegant primary sequence interrogation [ 9 , 10 ], atomic structures of different state conformations locked by pharmacological inhibitors [ 11 , 12 ] and site-directed mutagenesis screens [ 13 , 14 ], has confidently pinpointed the ligand binding residues of several characterized proteins in this family. This allows for an evaluation of coupling sequence adaptation to the transporting ligands. The transmembrane region of each SLC25 transporter is a structural and functional monomer of only approximately 300 amino acids with six transmembrane α-helices (threefold pseudo-symmetrical repeats of the two transmembrane helices called the “mito_carr” and “Solcar” domains) surrounding the central cavity. The ADP/ATP carrier crystal structures in both cytoplasmic-open (c-state) and matrix-open states (m-state), locked by two inhibitors bound at the ligand binding site, carboxyatractyloside and bongkrekic acid, respectively, highlight a conserved alternating-access transport mechanism that is triggered by a conformational change that occurs upon ligand binding at the central cavity [ 8 ]. Therefore, it is reasonable to speculate that the residues involved in ligand recognition and translocation would evolve and adapt for specific ligands that might be reflected by phylogenetic analysis.

Third, and most remarkably, the SLC25 family is highly evolutionarily conserved yet functionally diverse in eukaryotes. This family is present in all eukaryotic species (no bacterial and archaeal homologs have been identified so far), with only a few exceptions in protist species that have significantly reduced mitochondrial function, Giardia lamblia and Encephalitozoon cuniculi [ 15 ], or that have completely lost mitochondria, e.g., Monocercomonoides sp. [ 16 ]. We postulate that the SLC25 family might have massively expanded even before the last eukaryotic common ancestor and diversified into distinct transporters with different ligand specificities, subfamilies or orthologous groups. This is because (i) any genome that contains the SLC25 family is found to encode multiple SLC25 family genes, for instance, the human genome encodes 53, and even the distantly diverged apicomplexans contain about a dozen; (ii) in many reported cases [ 17 , 18 , 19 ], the corresponding mammalian ortholog can rescue the yeast SLC25 mutant phenotypes, suggesting human-to-yeast conservation; and (iii) previous phylogenetic analysis of SLC25 transporters within human and yeast genomes [ 20 , 21 ] already suggested that their protein sequences are clustered by function, specifically ligand specificity [ 21 ].

Here, to evaluate the sequence adaption for transporting ligands within the SLC25 family, we performed a phylogenetic analysis of SLC25 transporters from humans and commonly studied model organisms and annotated the tree based on the chemistry of the experimentally validated transporting ligands. We observed that for majority of the transporters, there exists a clustering of orthologous transporters across different species that transport the same ligand, suggesting an early divergence of these metabolite transporters as well as the coupling of sequence variation to ligand adaptation. They include ADP/ATP exchangers and transporters for CoA, carboxylates, glutathione, SAM and several amino acids, among others. In other cases, the sequence variation might be coupled to a conserved metabolite regulation mechanism or to other functional innovations, for instance, targeting different subcellular membranes, including outer mitochondrial membranes or peroxisomes. A lack of homology for several species-specific transporters is also noted. In summary, we explore the power of phylogenetic analysis in ligand prediction for the SLC25 transporter family, which might guide the “deorphanization” effort for some of the poorly characterized SLC25 transporters as well as provide an example for the exploration of other transporter families.

2. Materials and Methods

We chose the following five genomes, including commonly studied model organisms, to evaluate the SLC25 protein family: Saccharomyces cerevisiae (budding yeast, id: 4932), Caenorhabditis elegans (roundworm, id: 6239), Drosophila melanogaster (fruit fly, id: 7227), Danio rerio (zebrafish, id: 7955) and Homo sapiens (human, id: 9606). We reasoned that these organisms are diverse enough to represent different eukaryotic branches, and as model organisms, the sequences are more likely to be experimentally studied and thus suitable for our analysis.

SLC25 sequences from each genome were identified via a text-mining search in the UNIPROT database [ 22 ], using a combined “mito_carr” and “solcar” search into each organism via a taxonomy code (Data S1). We chose to carry out a text-mining search in UNIPROT over searching NCBI BLASTp/tBLASTn for the following reasons: first, the proteome annotations for these model organisms in UNIPROT are relatively complete, albeit with duplication and errors; and second, we found that “mito_carr” and “Solcar” domain predictions are of high accuracy. For instance, many SLC25 protein sequences from these model organisms are considered validated (“reviewed” in UNIPROT), including all 53 human SLC25s, all 35 yeast SLC25s and tens of worm, fly, and zebrafish SLC25s.

While validating the yeast sequences, we noticed that the Cmc1 protein from the S288c yeast strain ( D6W196 ) was curated as a truncated form of the protein due to a frameshift in position 403 in Strain S288c. We therefore replaced this sequence with the full-length sequence of the same protein from the CG379 yeast strain ( P0CI40 ).

Upon validating the yeast (35) and human (53) sequences, we then manually curated the SLC25 sequences in worm (49), fly (120) and zebrafish (111) using several rounds of multiple-sequence alignment (MUSCLE) [ 23 , 24 ] within each organism (Data S2). We (1) included all UNIPROT-“reviewed” sequences; (2) eliminated obvious duplicated sequences if the sequence identity <0.005; and (3) removed obvious truncated sequences (usually <200 amino acids in length). We chose 200 amino acids as a relatively loose cutoff to accommodate SLC25 proteins that might have truncated hydrophilic loops. However, all validated SLC25 protein sequences we curated are of approximately 300 amino acids or longer if they contain additional protein domains.

In summary, we included in our analysis 53 human, 35 yeast, 35 worm, 48 fly and 57 zebrafish SLC25 protein sequences. We acknowledge that our curation might contain errors for the worm, fly and zebrafish sequences, especially for paralogs within the same subfamily. First, for several subfamilies that are known to contain multiple paralogous genes, for instance, ADP/ATP exchangers and CMCs, multiple sequences might have identity values <0.01 but would either map to different chromosomal regions in tBLASTn or the mapping was of low confidence; therefore, the number of paralogs might be incorrect. Second, the zebrafish genome is known to have local genome duplication, so paralogs might be missing in our analysis. Regardless of the exact number of sequences, our analysis should sufficiently represent the complete functional diversity of the family.

We then manually trimmed all protein sequences to the regions that are predicted to encompass the three “Solcar” domains: the core transporter regions. For instance, the predicted EF-hand domains in CMCs and Aralars were removed. We then included the human MCU, another inner membrane channel, as the outgroup.

We aligned the protein sequences using MAFFT v7.505 [ 25 ] and determined the best substitution model (LG + F + G4) via ModelFinder [ 26 ]. We then used this model to construct a phylogenetic tree, using IQ-Tree v2.1.2. [ 27 ] with branch support values obtained via ultrafast bootstrapping from 10,000 replicates [ 28 ]. iTOL [ 29 ] was used to visualize and annotate the resulting tree, which we rooted using the human protein MCU as the outgroup.

To perform the phylogenetic analysis, we collected amino acid sequences via a text-mining search (using “mito_carr” and “Solcar” in the UNIPROT database) against each model organism using their taxonomy codes. These organisms included Homo sapiens (human), Saccharomyces cerevisiae (yeast), Caenorhabditis elegans (worm), Drosophila melanogaster (fly) and Danio rerio (zebrafish). We chose these model organisms because they are evolutionarily diverse and are likely to be experimentally studied and annotated. Upon manual curation (see method), we finalized the sequence entry, which included 53 human sequences, 57 zebrafish sequences, 48 fly sequences, 35 worm sequences and 35 sequences. The large numbers of SLC25 transporters in all model organisms are consistent with a putative massive gene family expansion prior to the time when these eukaryotic lineages diverged. We then performed a multiple sequence analysis, using a nonhomologous mitochondrial calcium uniporter sequence in human (MCU) as the outgroup, and constructed the phylogenetic tree with bootstrap values to highlight clade confidence (a bootstrap value > 70 denotes high confidence).

We then sought to functionally annotate the tree by color-coding major clades based on the chemistry of the transporting ligands identified for the known transporters in the clade. Specifically, the subfamily is manually annotated by ligand based on the biochemical activity of the well-characterized representative yeast or human SLC25 proteins in each clade and then expanded to the other SLC25 proteins in the clade with bootstrapping values > 90 ( Figure 1 and Figure S1 ). Indeed, the majority of the well-characterized paralogs and orthologs across all model organisms translocating the same ligand are well-clustered with extremely high levels of confidence (bootstrapping values > 90), followed by homologs translocating ligands with similar chemical structures. For instance, the well-characterized SLC25 ADP/ATP exchanger (also named AACs, ANTs, ANCs and ADTs) that include four human transporters (SLC25A4, SLC25A5, SLC25A6 and SLC25A31) and their orthologs are all clustered together and are within the nucleotide transporter clade. Because several recent reviews have already summarized the characterized SLC25 transporters [ 21 , 30 , 31 ], here, we will highlight a few recently identified transporters and transporters of poorly characterized functions or of uncertainty in the human genome, with the goal of guiding future functional characterizations.

Phylogenetic analysis of SLC25 mitochondrial transporter family members. All human (human), Danio rerio (DANRE), Caenorhabditis elegans (CAEEL), Drosophila melanogaster (DROME), and Saccharomyces cerevisiae (YEAST, or YEASX for CMC1, see the Materials and Methods) SLC25 family transporters were aligned, built into a tree, then color-annotated by the transporting ligands. Bold lines represent bootstrap values > 70.

3.1. Recently Characterized Transporters

Glutathione for SLC25A39 and SLC25A40

SLC25A39 was recently identified as the evolutionarily conserved, putative transporter for the major cellular antioxidant glutathione, the tripeptide in which the γ-peptide bond preserves the amino acid chemical group of the glutamate [ 32 , 33 ]. The phylogenetic tree supports SLC25A40 as the human paralog [ 32 ].

BCAAs for SLC25A44

The recently identified branched-chain amino acid (BCAA) transporter SLC25A44 [ 34 ] contains orthologs in animals (fly, worm and zebrafish) but no obvious orthologs in yeast.

Both the SLC25A39 and SLC25A44 clades are nested within a cluster of transporters (despite having low homology with the other groups) in which the majority translocate amino acids, supporting their putative identification.

NAD+ for SLC25A51 and SLC25A52

Recently identified putative human NAD+ transporters, SLC25A51 [ 35 , 36 , 37 ] and SLC25A52 [ 35 ], cluster within the same clade. This clade also contains orthologous genes in all animal model organisms but exhibits little homology with the yeast NAD transporters Ndt1/Yia6 and Ndt2/Yea6 [ 38 ]. It would be intriguing if fungi and animals independently evolved their ability to transport NAD cofactors, as well as their dependence on NAD-mediated OXPHOS to support mitochondrial bioenergetics. A homologous human transporter, SLC25A53, remains an orphan. This clade is adjacent to the majority of the nucleotide transporter clade, but a lack of high homology (bootstrap values < 70) might suggest that a homology search is not sufficient for guiding ligand characterization.

3.2. Transporters of Uncertainty

The evolutionarily conserved SLC25A32 subfamily has been proposed to transport both dinucleotide cofactor FAD and tetrahydrofolate (THF) cofactors supporting a mitochondrial one-carbon metabolism. While in vitro [ 39 ], mouse genetics [ 40 ] and cellular characterizations [ 41 , 42 , 43 ] supported its role in THF cofactor transport and one-carbon metabolism, this SLC25A32 clade’s homology to other nucleotide transporters might also support FAD transport [ 44 , 45 , 46 ].

The previously proposed putative glycine transporter SLC25A38 [ 47 , 48 ] was found to contain orthologs in zebrafish, yeast and human. This clade was recently proposed to also transport isopentenyl pyrophosphate (IPP), which is involved in CoQ biosynthesis (yeast ortholog Hem25, a fungi-specific function [ 49 ]), and to regulate other metabolite transport. The SLC25A38 clade appears to be within a majority amino-acid-transporting group.

3.3. Poorly Characterized Transporters

Peroxisomal SLC25A17

The only non-mitochondrial SLC25 protein, peroxisomal SLC25A17 [ 50 ], which is present in human, fruit fly, and zebrafish, does not exhibit homology of high confidence with other SLC25 transporters. Its clustering with the yeast peroxisomal nucleotide transporter Ant1 [ 51 ] cannot be validated via a bidirectional best hit (BBH) search. This lack of obvious homology might suggest an early divergence with potentially broader substrate specificity [ 50 ] and a situation in which sequence variation might not be coupled to ligand specificity but to subcellular targeting.

SLC25A34 and SLC25A35

The distinct SLC25A34 and SLC25A35 subfamily of completely unknown function contains human, fly, zebrafish and yeast orthologs, such as yeast Oac1 [ 52 ], but does not have any worm orthologs. The clade exhibits homology with the clade of dicarboxylate transporters SLC25A10 and SLC25A11 (bootstrap = 59), followed by homology with the U n C oupling P rotein subfamily UCP1-5 (SLC25A7, A8, A9, A14 and A30) (bootstrap = 95), in which dicarboxylate transport activities have been proposed for several UCPs [ 53 , 54 , 55 ]. Such insights might guide the characterization of these proteins.

The vertebrate-specific SLC25A43 (only in human and zebrafish) of completely unknown function sparked interest because the clade is nested within a majority nucleotide group with high confidence (bootstrap = 86). The clade’s high homology to ADP/ATP carriers (SLC25A4, A5, A6 and A31), CoA transporters (A16 and A42) and the nucleotide-importer SCAMC subfamily, followed by thiamine pyrophosphate transporters, might guide the deorphanization of SLC25A43.

Despite a close clustering of high confidence, we cannot validate the homology via BBH search between SLC25A43 and the yeast Ugo1, an outer mitochondrial membrane SLC25 protein that is important for mitochondrial fusion with unknown ligand significance [ 56 ]. We therefore suspect that this clustering might be an artifact due to long-branch attraction of unknown causes [ 57 ], and the SLC25A43 clade might be a vertebrate-specific innovation.

SLC25A45, SLC25A47 and SLC25A48

The homologous SLC25A45, SLC25A47 and SLC25A48 are three poorly characterized transporters that are clustered within a distinct clade within the amino acid transporters, separated (bootstrap = 83) but homologous (bootstrap = 78) with the putative basic amino acid transporter SLC25A29, followed by a homology with the carnitine transporter SLC25A20 and the ornithine transporters SLC25A15 and SLC25A2 (bootstrap = 100). Recent loss-of-function studies in mouse livers suggest that deleting the liver-specific [ 58 , 59 , 60 ] Slc25a47 leads to a reduction in respiration [ 58 ], an increase in the mitochondrial stress response [ 58 , 60 ] and an impaired lipid metabolism [ 59 ]. While the exact endogenous ligand is yet to be identified, our phylogenetic analysis does not support a nucleotide substrate using this family-wide conserved ligand recognition mechanism.

Outer mitochondrial membrane SLC25A46, MTCH1 and MTCH2

The three human outer mitochondrial membrane SLC25 proteins, SLC25A46, MTCH1 and MTCH2, are homologous with high levels of confidence with other animal sequences in worm, fly and zebrafish. A lack of homology with the yeast outer mitochondrial membrane protein Ugo1 might suggest two independent evolutionary innovations to utilize the inner membrane SLC25 protein scaffold for new outer membrane function. The recently proposed novel role of MTCH2 as an outer mitochondrial membrane insertase [ 61 ] is intriguing, and future studies are required to bridge this biochemical activity with the previously proposed roles of MTCH2 in membrane fusion [ 62 , 63 ] and apoptosis [ 64 ] in yeast and in animals. The significance of potential metabolite binding at the family-wide conserved ligand binding pocket is yet to be explored.

4. Discussion

Here, we performed a phylogenetic analysis of SLC25 family transporters from common model organisms to evaluate the power of homology search in guiding ligand characterization. Our analysis exhibited an extremely high degree of homology between SLC25 transporters across evolution that transport the same ligand (bootstrapping value > 90), consistent with an early functional divergence of SLC25 proteins. Consistent with previous phylogenetic analyses [ 20 , 21 ], we also observed a high degree of homology between SLC25 proteins transporting ligands with similar chemistries, e.g., nucleotides, amino acids and carboxylates (bootstrapping value usually >50), supporting the coupling of sequence variation to functional divergence. The ability of the homology search to guide ligand prediction is promising for several remaining “orphan” SLC25 transporters and is discussed case-by-base.

While several phylogenetic analyses have been performed on automatically collected SLC25 sequences across a broad range of eukaryotic taxa [ 65 , 66 , 67 ], our analysis, which focused on a few model organisms, provides unique insights to guide future functional annotation. Because the model organism proteomes are well curated, we were able to carefully exhaust all SLC25s in each species and more importantly, immediately distinguish the evolutionarily conserved SLC25s from the SLC25s that might be due to recent innovation in vertebrates or in mammals. Unsurprisingly, the biochemical activities of most evolutionarily conserved SLC25s have been characterized, and a majority of the poorly characterized transporters are only present in certain species, suggesting they are dispensable for central and conserved mitochondrial metabolism in animals—an important insight to interpret for any future research detecting their biochemical activities in the context of the human mitochondrial metabolism.

Our analysis should not be affected by the potentially incorrect number of SLC25 family proteins in each species because the error should only occur for species-specific paralogs for which we cannot distinguish whether certain transporter sequences have inaccurate annotations or are taxa-specific gene duplications. A more complete analysis might benefit from the inclusion of other model organisms, including the plant Arabidopsis thaliana , house mouse, Mus musculus , and western clawed frog, Xenopus tropicalis (often used for the study of ion channels). For recently innovated SLC25 proteins, a phylogenetic analysis focusing on sequenced vertebrate [ 68 ] or mammalian genomes [ 69 ] might inform the understanding of their adaptative evolution in human physiology.

Several limitations to utilizing homology search for ligand characterization are noted. First, singleton transporters with little homology with other transporters provide little guidance toward their characterization. Examples of this include the peroxisome SLC25A17 clade (discussed above) and many species-specific transporters, for instance, the fruit fly MME1 ( Q9VM51 , annotated as “Mitochondrial Magnesium Exporter 1”) [ 70 ] and the COLT of unknown function ( Q9VQG4 , annotated as “Congested-like trachea protein”) [ 71 ], both of which are within the amino acid transporter clade. Second, we highlighted that homology-based sequence variation cannot distinguish between adaptation to new ligands and adaptation to different subcellular organelle targeting or to other moonlighting functions. For instance, the homology among the U n C oupling P roteins (UCPs) might potentially suggest an adapted metabolite regulation mechanism instead of an adaptation to transported ligands—for example, the regulation of UCP1 by purine nucleotides—demonstrated via structure [ 72 , 73 ] and molecular simulation [ 74 ].

A phylogenetic analysis could potentially guide experimental ligand characterization efforts for certain SLC25 transporters as an orthologous strategy to in vitro proteoliposome-based transport assays, cell-based assays and in vivo studies. Other molecular evolution approaches could also provide exciting insights [ 66 ]. A comprehensive evaluation of how a homology search and phylogenetic analysis could guide deorphanization efforts probably requires a “dream world” scenario in which experimentally validated functional annotation is available for every C luster of O rthologous G roup (COG) in bacteria and in eukaryotes [ 75 ].

Acknowledgments

We thank Xiaojian Shi and other members of the Shen lab for the fruitful discussion and feedback.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/biom13091314/s1 , Figure S1: Phylogenetic analysis of the SLC25 mitochondrial transporter family members with bootstrap values; Data S1: SLC25 transporter protein sequence file; Data S2: SLC25 transporter protein alignment file.

Author Contributions

Conceptualization, H.S. and K.L.B.; analysis and investigation, K.L.B., R.V.S. and H.S.; writing—original draft preparation, K.L.B. and H.S.; editing, K.L.B., R.V.S. and H.S.; supervision, H.S. All authors have read and agreed to the published version of the manuscript.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Data availability statement.

Sequence and alignment data files are provided within the paper.

Conflicts of Interest

The authors declare no conflict of interest.

Funding Statement

This research was funded by the Yale School Medicine and Yale West Campus startup (H.S.) and NIH grant R35GM150619 (H.S.).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

• 1. Ellens K.W., Christian N., Singh C., Satagopam V.P., May P., Linster C.L. Confronting the catalytic dark matter encoded by sequenced genomes. Nucleic Acids Res. 2017;45:11495–11514. doi: 10.1093/nar/gkx937. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 2. Galperin M.Y., Koonin E.V. Divergence and convergence in enzyme evolution. J. Biol. Chem. 2012;287:21–28. doi: 10.1074/jbc.R111.241976. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 3. Khersonsky O., Tawfik D.S. Enzyme promiscuity: A mechanistic and evolutionary perspective. Annu. Rev. Biochem. 2010;79:471–505. doi: 10.1146/annurev-biochem-030409-143718. [ DOI ] [ PubMed ] [ Google Scholar ]
• 4. Walker J.E. The mitochondrial transporter family. Curr. Opin. Struct. Biol. 1992;2:519–526. doi: 10.1016/0959-440X(92)90081-H. [ DOI ] [ Google Scholar ]
• 5. Walker J.E., Runswick M.J. The mitochondrial transport protein superfamily. J. Bioenerg. Biomembr. 1993;25:435–446. doi: 10.1007/BF01108401. [ DOI ] [ PubMed ] [ Google Scholar ]
• 6. Palmieri F. Mitochondrial carrier proteins. FEBS Lett. 1994;346:48–54. doi: 10.1016/0014-5793(94)00329-7. [ DOI ] [ PubMed ] [ Google Scholar ]
• 7. Palmieri F. The mitochondrial transporter family (SLC25): Physiological and pathological implications. Pflugers Arch. 2004;447:689–709. doi: 10.1007/s00424-003-1099-7. [ DOI ] [ PubMed ] [ Google Scholar ]
• 8. Ruprecht J.J., Kunji E.R.S. The SLC25 Mitochondrial Carrier Family: Structure and Mechanism. Trends Biochem. Sci. 2020;45:244–258. doi: 10.1016/j.tibs.2019.11.001. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 9. Robinson A.J., Overy C., Kunji E.R. The mechanism of transport by mitochondrial carriers based on analysis of symmetry. Proc. Natl. Acad. Sci. USA. 2008;105:17766–17771. doi: 10.1073/pnas.0809580105. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 10. Robinson A.J., Kunji E.R. Mitochondrial carriers in the cytoplasmic state have a common substrate binding site. Proc. Natl. Acad. Sci. USA. 2006;103:2617–2622. doi: 10.1073/pnas.0509994103. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 11. Pebay-Peyroula E., Dahout-Gonzalez C., Kahn R., Trezeguet V., Lauquin G.J., Brandolin G. Structure of mitochondrial ADP/ATP carrier in complex with carboxyatractyloside. Nature. 2003;426:39–44. doi: 10.1038/nature02056. [ DOI ] [ PubMed ] [ Google Scholar ]
• 12. Ruprecht J.J., King M.S., Zogg T., Aleksandrova A.A., Pardon E., Crichton P.G., Steyaert J., Kunji E.R.S. The Molecular Mechanism of Transport by the Mitochondrial ADP/ATP Carrier. Cell. 2019;176:435–447.e415. doi: 10.1016/j.cell.2018.11.025. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 13. Mavridou V., King M.S., Tavoulari S., Ruprecht J.J., Palmer S.M., Kunji E.R.S. Substrate binding in the mitochondrial ADP/ATP carrier is a step-wise process guiding the structural changes in the transport cycle. Nat. Commun. 2022;13:3585. doi: 10.1038/s41467-022-31366-5. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 14. Monne M., Miniero D.V., Daddabbo L., Robinson A.J., Kunji E.R., Palmieri F. Substrate specificity of the two mitochondrial ornithine carriers can be swapped by single mutation in substrate binding site. J. Biol. Chem. 2012;287:7925–7934. doi: 10.1074/jbc.M111.324855. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 15. Tsaousis A.D., Kunji E.R., Goldberg A.V., Lucocq J.M., Hirt R.P., Embley T.M. A novel route for ATP acquisition by the remnant mitochondria of Encephalitozoon cuniculi. Nature. 2008;453:553–556. doi: 10.1038/nature06903. [ DOI ] [ PubMed ] [ Google Scholar ]
• 16. Karnkowska A., Vacek V., Zubacova Z., Treitli S.C., Petrzelkova R., Eme L., Novak L., Zarsky V., Barlow L.D., Herman E.K., et al. A Eukaryote without a Mitochondrial Organelle. Curr. Biol. 2016;26:1274–1284. doi: 10.1016/j.cub.2016.03.053. [ DOI ] [ PubMed ] [ Google Scholar ]
• 17. Prohl C., Pelzer W., Diekert K., Kmita H., Bedekovics T., Kispal G., Lill R. The yeast mitochondrial carrier Leu5p and its human homologue Graves’ disease protein are required for accumulation of coenzyme A in the matrix. Mol. Cell. Biol. 2001;21:1089–1097. doi: 10.1128/MCB.21.4.1089-1097.2001. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 18. Di Noia M.A., Todisco S., Cirigliano A., Rinaldi T., Agrimi G., Iacobazzi V., Palmieri F. The human SLC25A33 and SLC25A36 genes of solute carrier family 25 encode two mitochondrial pyrimidine nucleotide transporters. J. Biol. Chem. 2014;289:33137–33148. doi: 10.1074/jbc.M114.610808. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 19. Nilsson R., Schultz I.J., Pierce E.L., Soltis K.A., Naranuntarat A., Ward D.M., Baughman J.M., Paradkar P.N., Kingsley P.D., Culotta V.C., et al. Discovery of genes essential for heme biosynthesis through large-scale gene expression analysis. Cell Metab. 2009;10:119–130. doi: 10.1016/j.cmet.2009.06.012. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 20. Palmieri F., Agrimi G., Blanco E., Castegna A., Di Noia M.A., Iacobazzi V., Lasorsa F.M., Marobbio C.M., Palmieri L., Scarcia P., et al. Identification of mitochondrial carriers in Saccharomyces cerevisiae by transport assay of reconstituted recombinant proteins. Biochim. Biophys. Acta. 2006;1757:1249–1262. doi: 10.1016/j.bbabio.2006.05.023. [ DOI ] [ PubMed ] [ Google Scholar ]
• 21. Palmieri F. The mitochondrial transporter family SLC25: Identification, properties and physiopathology. Mol. Asp. Med. 2013;34:465–484. doi: 10.1016/j.mam.2012.05.005. [ DOI ] [ PubMed ] [ Google Scholar ]
• 22. UniProt C. UniProt: The Universal Protein Knowledgebase in 2023. Nucleic Acids Res. 2023;51:D523–D531. doi: 10.1093/nar/gkac1052. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 23. Madeira F., Pearce M., Tivey A.R.N., Basutkar P., Lee J., Edbali O., Madhusoodanan N., Kolesnikov A., Lopez R. Search and sequence analysis tools services from EMBL-EBI in 2022. Nucleic Acids Res. 2022;50:W276–W279. doi: 10.1093/nar/gkac240. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 24. Edgar R.C. MUSCLE: Multiple sequence alignment with high accuracy and high throughput. Nucleic Acids Res. 2004;32:1792–1797. doi: 10.1093/nar/gkh340. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 25. Katoh K., Standley D.M. MAFFT multiple sequence alignment software version 7: Improvements in performance and usability. Mol. Biol. Evol. 2013;30:772–780. doi: 10.1093/molbev/mst010. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 26. Kalyaanamoorthy S., Minh B.Q., Wong T.K.F., von Haeseler A., Jermiin L.S. ModelFinder: Fast model selection for accurate phylogenetic estimates. Nat. Methods. 2017;14:587–589. doi: 10.1038/nmeth.4285. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 27. Nguyen L.T., Schmidt H.A., von Haeseler A., Minh B.Q. IQ-TREE: A fast and effective stochastic algorithm for estimating maximum-likelihood phylogenies. Mol. Biol. Evol. 2015;32:268–274. doi: 10.1093/molbev/msu300. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 28. Hoang D.T., Chernomor O., von Haeseler A., Minh B.Q., Vinh L.S. UFBoot2: Improving the Ultrafast Bootstrap Approximation. Mol. Biol. Evol. 2018;35:518–522. doi: 10.1093/molbev/msx281. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 29. Letunic I., Bork P. Interactive Tree Of Life (iTOL) v5: An online tool for phylogenetic tree display and annotation. Nucleic Acids Res. 2021;49:W293–W296. doi: 10.1093/nar/gkab301. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 30. Kunji E.R.S., King M.S., Ruprecht J.J., Thangaratnarajah C. The SLC25 Carrier Family: Important Transport Proteins in Mitochondrial Physiology and Pathology. Physiology. 2020;35:302–327. doi: 10.1152/physiol.00009.2020. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 31. Cunningham C.N., Rutter J. 20,000 picometers under the OMM: Diving into the vastness of mitochondrial metabolite transport. EMBO Rep. 2020;21:e50071. doi: 10.15252/embr.202050071. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 32. Wang Y., Yen F.S., Zhu X.G., Timson R.C., Weber R., Xing C., Liu Y., Allwein B., Luo H., Yeh H.W., et al. SLC25A39 is necessary for mitochondrial glutathione import in mammalian cells. Nature. 2021;599:136–140. doi: 10.1038/s41586-021-04025-w. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 33. Shi X., Reinstadler B., Shah H., To T.L., Byrne K., Summer L., Calvo S.E., Goldberger O., Doench J.G., Mootha V.K., et al. Combinatorial GxGxE CRISPR screen identifies SLC25A39 in mitochondrial glutathione transport linking iron homeostasis to OXPHOS. Nat. Commun. 2022;13:2483. doi: 10.1038/s41467-022-30126-9. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 34. Yoneshiro T., Wang Q., Tajima K., Matsushita M., Maki H., Igarashi K., Dai Z., White P.J., McGarrah R.W., Ilkayeva O.R., et al. BCAA catabolism in brown fat controls energy homeostasis through SLC25A44. Nature. 2019;572:614–619. doi: 10.1038/s41586-019-1503-x. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 35. Luongo T.S., Eller J.M., Lu M.J., Niere M., Raith F., Perry C., Bornstein M.R., Oliphint P., Wang L., McReynolds M.R., et al. SLC25A51 is a mammalian mitochondrial NAD+ transporter. Nature. 2020;588:174–179. doi: 10.1038/s41586-020-2741-7. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 36. Kory N., Uit de Bos J., van der Rijt S., Jankovic N., Gura M., Arp N., Pena I.A., Prakash G., Chan S.H., Kunchok T., et al. MCART1/SLC25A51 is required for mitochondrial NAD transport. Sci. Adv. 2020;6:eabe5310. doi: 10.1126/sciadv.abe5310. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 37. Girardi E., Agrimi G., Goldmann U., Fiume G., Lindinger S., Sedlyarov V., Srndic I., Gurtl B., Agerer B., Kartnig F., et al. Epistasis-driven identification of SLC25A51 as a regulator of human mitochondrial NAD import. Nat. Commun. 2020;11:6145. doi: 10.1038/s41467-020-19871-x. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 38. Todisco S., Agrimi G., Castegna A., Palmieri F. Identification of the mitochondrial NAD+ transporter in Saccharomyces cerevisiae. J. Biol. Chem. 2006;281:1524–1531. doi: 10.1074/jbc.M510425200. [ DOI ] [ PubMed ] [ Google Scholar ]
• 39. Lawrence S.A., Hackett J.C., Moran R.G. Tetrahydrofolate recognition by the mitochondrial folate transporter. J. Biol. Chem. 2011;286:31480–31489. doi: 10.1074/jbc.M111.272187. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 40. Kim J., Lei Y., Guo J., Kim S.E., Wlodarczyk B.J., Cabrera R.M., Lin Y.L., Nilsson T.K., Zhang T., Ren A., et al. Formate rescues neural tube defects caused by mutations in Slc25a32. Proc. Natl. Acad. Sci. USA. 2018;115:4690–4695. doi: 10.1073/pnas.1800138115. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 41. McCarthy E.A., Titus S.A., Taylor S.M., Jackson-Cook C., Moran R.G. A mutation inactivating the mitochondrial inner membrane folate transporter creates a glycine requirement for survival of chinese hamster cells. J. Biol. Chem. 2004;279:33829–33836. doi: 10.1074/jbc.M403677200. [ DOI ] [ PubMed ] [ Google Scholar ]
• 42. Titus S.A., Moran R.G. Retrovirally mediated complementation of the glyB phenotype. Cloning of a human gene encoding the carrier for entry of folates into mitochondria. J. Biol. Chem. 2000;275:36811–36817. doi: 10.1074/jbc.M005163200. [ DOI ] [ PubMed ] [ Google Scholar ]
• 43. Zheng Y., Lin T.Y., Lee G., Paddock M.N., Momb J., Cheng Z., Li Q., Fei D.L., Stein B.D., Ramsamooj S., et al. Mitochondrial One-Carbon Pathway Supports Cytosolic Folate Integrity in Cancer Cells. Cell. 2018;175:1546–1560.e17. doi: 10.1016/j.cell.2018.09.041. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 44. Spaan A.N., Ijlst L., van Roermund C.W., Wijburg F.A., Wanders R.J., Waterham H.R. Identification of the human mitochondrial FAD transporter and its potential role in multiple acyl-CoA dehydrogenase deficiency. Mol. Genet. Metab. 2005;86:441–447. doi: 10.1016/j.ymgme.2005.07.014. [ DOI ] [ PubMed ] [ Google Scholar ]
• 45. Hellebrekers D., Sallevelt S., Theunissen T.E.J., Hendrickx A.T.M., Gottschalk R.W., Hoeijmakers J.G.J., Habets D.D., Bierau J., Schoonderwoerd K.G., Smeets H.J.M. Novel SLC25A32 mutation in a patient with a severe neuromuscular phenotype. Eur. J. Hum. Genet. 2017;25:886–888. doi: 10.1038/ejhg.2017.62. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 46. Schiff M., Veauville-Merllie A., Su C.H., Tzagoloff A., Rak M., Ogier de Baulny H., Boutron A., Smedts-Walters H., Romero N.B., Rigal O., et al. SLC25A32 Mutations and Riboflavin-Responsive Exercise Intolerance. N. Engl. J. Med. 2016;374:795–797. doi: 10.1056/NEJMc1513610. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 47. Lunetti P., Damiano F., De Benedetto G., Siculella L., Pennetta A., Muto L., Paradies E., Marobbio C.M., Dolce V., Capobianco L. Characterization of Human and Yeast Mitochondrial Glycine Carriers with Implications for Heme Biosynthesis and Anemia. J. Biol. Chem. 2016;291:19746–19759. doi: 10.1074/jbc.M116.736876. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 48. Guernsey D.L., Jiang H., Campagna D.R., Evans S.C., Ferguson M., Kellogg M.D., Lachance M., Matsuoka M., Nightingale M., Rideout A., et al. Mutations in mitochondrial carrier family gene SLC25A38 cause nonsyndromic autosomal recessive congenital sideroblastic anemia. Nat. Genet. 2009;41:651–653. doi: 10.1038/ng.359. [ DOI ] [ PubMed ] [ Google Scholar ]
• 49. Tai J., Guerra R.M., Rogers S.W., Fang Z., Muehlbauer L.K., Shishkova E., Overmyer K.A., Coon J.J., Pagliarini D.J. Hem25p is a mitochondrial IPP transporter. bioRxiv. 2023 doi: 10.1101/2023.03.14.532620. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 50. Agrimi G., Russo A., Scarcia P., Palmieri F. The human gene SLC25A17 encodes a peroxisomal transporter of coenzyme A, FAD and NAD+ Biochem. J. 2012;443:241–247. doi: 10.1042/BJ20111420. [ DOI ] [ PubMed ] [ Google Scholar ]
• 51. Palmieri L., Rottensteiner H., Girzalsky W., Scarcia P., Palmieri F., Erdmann R. Identification and functional reconstitution of the yeast peroxisomal adenine nucleotide transporter. EMBO J. 2001;20:5049–5059. doi: 10.1093/emboj/20.18.5049. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 52. Palmieri L., Vozza A., Agrimi G., De Marco V., Runswick M.J., Palmieri F., Walker J.E. Identification of the yeast mitochondrial transporter for oxaloacetate and sulfate. J. Biol. Chem. 1999;274:22184–22190. doi: 10.1074/jbc.274.32.22184. [ DOI ] [ PubMed ] [ Google Scholar ]
• 53. Gorgoglione R., Porcelli V., Santoro A., Daddabbo L., Vozza A., Monne M., Di Noia M.A., Palmieri L., Fiermonte G., Palmieri F. The human uncoupling proteins 5 and 6 (UCP5/SLC25A14 and UCP6/SLC25A30) transport sulfur oxyanions, phosphate and dicarboxylates. Biochim. Biophys. Acta—Bioenerg. 2019;1860:724–733. doi: 10.1016/j.bbabio.2019.07.010. [ DOI ] [ PubMed ] [ Google Scholar ]
• 54. Monne M., Daddabbo L., Gagneul D., Obata T., Hielscher B., Palmieri L., Miniero D.V., Fernie A.R., Weber A.P.M., Palmieri F. Uncoupling proteins 1 and 2 (UCP1 and UCP2) from Arabidopsis thaliana are mitochondrial transporters of aspartate, glutamate, and dicarboxylates. J. Biol. Chem. 2018;293:4213–4227. doi: 10.1074/jbc.RA117.000771. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 55. Vozza A., Parisi G., De Leonardis F., Lasorsa F.M., Castegna A., Amorese D., Marmo R., Calcagnile V.M., Palmieri L., Ricquier D., et al. UCP2 transports C4 metabolites out of mitochondria, regulating glucose and glutamine oxidation. Proc. Natl. Acad. Sci. USA. 2014;111:960–965. doi: 10.1073/pnas.1317400111. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 56. Sesaki H., Jensen R.E. UGO1 encodes an outer membrane protein required for mitochondrial fusion. J. Cell Biol. 2001;152:1123–1134. doi: 10.1083/jcb.152.6.1123. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 57. Bergsten J. A review of long-branch attraction. Cladistics. 2005;21:163–193. doi: 10.1111/j.1096-0031.2005.00059.x. [ DOI ] [ PubMed ] [ Google Scholar ]
• 58. Bresciani N., Demagny H., Lemos V., Pontanari F., Li X., Sun Y., Li H., Perino A., Auwerx J., Schoonjans K. The Slc25a47 locus is a novel determinant of hepatic mitochondrial function implicated in liver fibrosis. J. Hepatol. 2022;77:1071–1082. doi: 10.1016/j.jhep.2022.05.040. [ DOI ] [ PubMed ] [ Google Scholar ]
• 59. Cheng L., Deepak R., Wang G., Meng Z., Tao L., Xie M., Chi W., Zhang Y., Yang M., Liao Y., et al. Hepatic mitochondrial NAD+ transporter SLC25A47 activates AMPKalpha mediating lipid metabolism and tumorigenesis. Hepatology. 2023 doi: 10.1097/HEP.0000000000000314. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 60. Yook J.S., Taxin Z.H., Yuan B., Oikawa S., Auger C., Mutlu B., Puigserver P., Hui S., Kajimura S. The SLC25A47 locus controls gluconeogenesis and energy expenditure. Proc. Natl. Acad. Sci. USA. 2023;120:e2216810120. doi: 10.1073/pnas.2216810120. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 61. Guna A., Stevens T.A., Inglis A.J., Replogle J.M., Esantsi T.K., Muthukumar G., Shaffer K.C.L., Wang M.L., Pogson A.N., Jones J.J., et al. MTCH2 is a mitochondrial outer membrane protein insertase. Science. 2022;378:317–322. doi: 10.1126/science.add1856. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 62. Bahat A., Goldman A., Zaltsman Y., Khan D.H., Halperin C., Amzallag E., Krupalnik V., Mullokandov M., Silberman A., Erez A., et al. MTCH2-mediated mitochondrial fusion drives exit from naive pluripotency in embryonic stem cells. Nat. Commun. 2018;9:5132. doi: 10.1038/s41467-018-07519-w. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 63. Labbe K., Mookerjee S., Le Vasseur M., Gibbs E., Lerner C., Nunnari J. The modified mitochondrial outer membrane carrier MTCH2 links mitochondrial fusion to lipogenesis. J. Cell Biol. 2021;220:e202103122. doi: 10.1083/jcb.202103122. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 64. Zaltsman Y., Shachnai L., Yivgi-Ohana N., Schwarz M., Maryanovich M., Houtkooper R.H., Vaz F.M., De Leonardis F., Fiermonte G., Palmieri F., et al. MTCH2/MIMP is a major facilitator of tBID recruitment to mitochondria. Nat. Cell Biol. 2010;12:553–562. doi: 10.1038/ncb2057. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 65. Gong M., Li J., Wang M., Wang J., Zen K., Zhang C.Y. The evolutionary trajectory of mitochondrial carrier family during metazoan evolution. BMC Evol. Biol. 2010;10:282. doi: 10.1186/1471-2148-10-282. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 66. Monne M., Cianciulli A., Panaro M.A., Calvello R., De Grassi A., Palmieri L., Mitolo V., Palmieri F. New Insights into the Evolution and Gene Structure of the Mitochondrial Carrier Family Unveiled by Analyzing the Frequent and Conserved Intron Positions. Mol. Biol. Evol. 2023;40:msad051. doi: 10.1093/molbev/msad051. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 67. Zhu X., Boulet A., Buckley K.M., Phillips C.B., Gammon M.G., Oldfather L.E., Moore S.A., Leary S.C., Cobine P.A. Mitochondrial copper and phosphate transporter specificity was defined early in the evolution of eukaryotes. eLife. 2021;10:e64690. doi: 10.7554/eLife.64690. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 68. Rhie A., McCarthy S.A., Fedrigo O., Damas J., Formenti G., Koren S., Uliano-Silva M., Chow W., Fungtammasan A., Kim J., et al. Towards complete and error-free genome assemblies of all vertebrate species. Nature. 2021;592:737–746. doi: 10.1038/s41586-021-03451-0. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 69. Vignieri S. Zoonomia. Science. 2023;380:356–357. doi: 10.1126/science.adi1599. [ DOI ] [ PubMed ] [ Google Scholar ]
• 70. Cui Y., Zhao S., Wang X., Zhou B. A novel Drosophila mitochondrial carrier protein acts as a Mg2+ exporter in fine-tuning mitochondrial Mg2+ homeostasis. Biochim. Biophys. Acta. 2016;1863:30–39. doi: 10.1016/j.bbamcr.2015.10.004. [ DOI ] [ PubMed ] [ Google Scholar ]
• 71. Hartenstein K., Sinha P., Mishra A., Schenkel H., Torok I., Mechler B.M. The congested-like tracheae gene of Drosophila melanogaster encodes a member of the mitochondrial carrier family required for gas-filling of the tracheal system and expansion of the wings after eclosion. Genetics. 1997;147:1755–1768. doi: 10.1093/genetics/147.4.1755. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 72. Jones S.A., Gogoi P., Ruprecht J.J., King M.S., Lee Y., Zogg T., Pardon E., Chand D., Steimle S., Copeman D.M., et al. Structural basis of purine nucleotide inhibition of human uncoupling protein 1. Sci. Adv. 2023;9:eadh4251. doi: 10.1126/sciadv.adh4251. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 73. Kang Y., Chen L. Structural basis for the binding of DNP and purine nucleotides onto UCP1. Nature. 2023;620:226–231. doi: 10.1038/s41586-023-06332-w. [ DOI ] [ PubMed ] [ Google Scholar ]
• 74. Gagelin A., Largeau C., Masscheleyn S., Piel M.S., Calderon-Mora D., Bouillaud F., Henin J., Miroux B. Molecular determinants of inhibition of UCP1-mediated respiratory uncoupling. Nat. Commun. 2023;14:2594. doi: 10.1038/s41467-023-38219-9. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 75. Koonin E.V., Fedorova N.D., Jackson J.D., Jacobs A.R., Krylov D.M., Makarova K.S., Mazumder R., Mekhedov S.L., Nikolskaya A.N., Rao B.S., et al. A comprehensive evolutionary classification of proteins encoded in complete eukaryotic genomes. Genome Biol. 2004;5:R7. doi: 10.1186/gb-2004-5-2-r7. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

• View on publisher site
• PDF (625.6 KB)
• Collections

Similar articles

Cited by other articles, links to ncbi databases.

• Download .nbib .nbib
• Format: AMA APA MLA NLM

Add to Collections